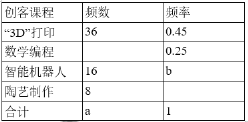
题目内容
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
【答案】(1)甲、乙工程队每天能完成绿化的面积分别是![]() 、
、![]() ;(2)
;(2)![]() ;(3)安排甲队施工
;(3)安排甲队施工![]() 天,乙队施工
天,乙队施工![]() 天,施工总费用最低,最低费用为
天,施工总费用最低,最低费用为![]() 万元.
万元.
【解析】
(1)设乙工程队每天能完成绿化的面积是![]() m2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列方程求解;
m2,根据在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,列方程求解;
(2)根据题意得到100x+50y=2400,整理得:y=-2x+48,即可解答;
(3)根据甲乙两队施工的总天数不超过30天,得到x≥18,设施工总费用为w元,根据题意得:![]() ,根据一次函数的性质,即可解答.
,根据一次函数的性质,即可解答.
(1)设乙工程队每天能完成绿化面积是![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,
经检验,![]() 是原方程的解,
是原方程的解,
则甲工程队每天能完成绿化的面积是![]()
答:甲、乙工程队每天能完成绿化的面积分别是![]() 、
、![]() ;
;
(2)根据题意得:![]() ,
,
整理得:![]() ,
,
∴y与x的函数解析式为:![]() .
.
(3)∵甲乙两队施工的总天数不超过30天,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
设施工总费用为![]() 元,根据题意得:
元,根据题意得:
![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
当![]() 时,
时,![]() 有最小值,最小值为
有最小值,最小值为![]() 万元,
万元,
此时,![]() ,
,
答:安排甲队施工![]() 天,乙队施工
天,乙队施工![]() 天,施工总费用最低,最低费用为
天,施工总费用最低,最低费用为![]() 万元.
万元.

 第1卷单元月考期中期末系列答案
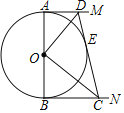
第1卷单元月考期中期末系列答案【题目】如图,在⊙![]() 中,AB是直径,BC是弦,BC=BD,连接CD交⊙
中,AB是直径,BC是弦,BC=BD,连接CD交⊙![]() 于点E,∠BCD=∠DBE.
于点E,∠BCD=∠DBE.
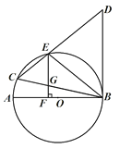
(1)求证:BD是⊙![]() 的切线.
的切线.
(2)过点E作EF⊥AB于F,交BC于G,已知DE=![]() ,EG=3,求BG的长.
,EG=3,求BG的长.