题目内容
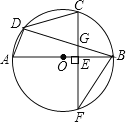
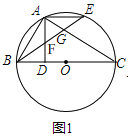
【题目】如图1，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，
，BE分别交AD、AC于点F、G．
（1）判断△FAG的形状，并说明理由；
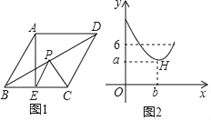
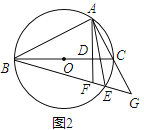
（2）如图2，若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由；
（3）在（2）的条件下，若BG＝26，BD﹣DF＝7，求AB的长．
【答案】（1）等腰三角形，理由见解析；（2）成立，理由见解析；（3）
．
【解析】
（1）首先根据圆周角定理及垂直的定义得到
，
，从而得到
，然后利用等弧对等角、等角对等边等知识得到
，从而证得
，判定等腰三角形；
（2）成立，证明方法同（1）；
（3）首先根据上题得到
，从而利用已知条件得到
，然后利用勾股定理得到
，
，从而求得
，最后求得
解：（1）结论：△FAG是等腰三角形；
理由：如图1，
为直径，
，
，，
，
，
，
，
，
，
，
，
，
是等腰三角形；
（2）（1）中的结论成立；
为直径，，
，，
，
，
，
，
，
，，
，
，
是等腰三角形；
（3）由（2）得：，
，
，
解得：，，
，
．
练习册系列答案
相关题目
【题目】如图，在⊙
中，AB是直径，BC是弦，BC=BD，连接CD交⊙于点E，∠BCD=∠DBE.
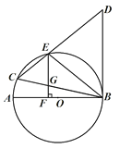
（1）求证：BD是⊙的切线.
（2）过点E作EF⊥AB于F，交BC于G，已知DE=
，EG=3，求BG的长.
