题目内容
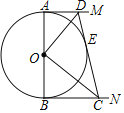
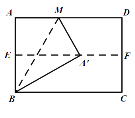
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM,若矩形纸片的宽AB=4,则折痕BM的长为( )
A.![]() B.
B.![]() C.8D.
C.8D.![]()
【答案】A
【解析】
根据折叠性质可得BE=![]() AB,A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,可得∠EA′B=30°,根据直角三角形两锐角互余可得∠EBA′=60°,进而可得∠ABM=30°,在Rt△ABM中,利用∠ABM的余弦求出BM的长即可.
AB,A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,可得∠EA′B=30°,根据直角三角形两锐角互余可得∠EBA′=60°,进而可得∠ABM=30°,在Rt△ABM中,利用∠ABM的余弦求出BM的长即可.
∵对折矩形纸片ABCD,使AD与BC重合,AB=4,
∴BE=![]() AB=2,∠BEF=90°,
AB=2,∠BEF=90°,
∵把纸片展平,再一次折叠纸片,使点A落在EF上的点A’处,并使折痕经过点B,
∴A′B=AB=4,∠BA′M=∠A=90°,∠ABM=∠MBA′,
∴∠EA′B=30°,
∴∠EBA′=60°,
∴∠ABM=30°,
∴在Rt△ABM中,AB=BM![]() cos∠ABM,即4=BM
cos∠ABM,即4=BM![]() cos30°,
cos30°,
解得:BM=![]() ,
,
故选A.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目