题目内容
如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.

(1)求证:DP∥AB;
(2)若AC=6,BC=8,求线段PD的长.

(1)求证:DP∥AB;
(2)若AC=6,BC=8,求线段PD的长.
解:(1)证明:如图,连接OD,
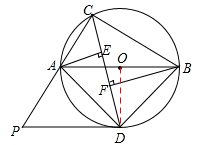
∵AB为⊙O的直径,∴∠ACB=90°。
∵∠ACB的平分线交⊙O于点D,∴∠ACD=∠BCD=45°。
∴∠DAB=∠ABD=45°。∴△DAB为等腰直角三角形。
∴DO⊥AB。
∵PD为⊙O的切线,∴OD⊥PD。
∴DP∥AB。
(2)在Rt△ACB中,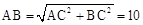 ,
,
∵△DAB为等腰直角三角形,∴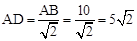 。
。
∵AE⊥CD,∴△ACE为等腰直角三角形。∴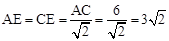 。
。
在Rt△AED中,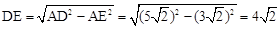 ,
,
∴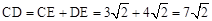 。
。
∵AB∥PD,∴∠PDA=∠DAB=45°。∴∠PAD=∠PCD。
又∵∠DPA=∠CPD,∴△PDA∽△PCD。∴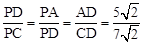 。
。
∴PA= PD,PC=
PD,PC=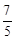 PD。
PD。
又∵PC=PA+AC,∴ PD+6=
PD+6=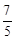 PD,解得PD=
PD,解得PD= 。
。

∵AB为⊙O的直径,∴∠ACB=90°。
∵∠ACB的平分线交⊙O于点D,∴∠ACD=∠BCD=45°。
∴∠DAB=∠ABD=45°。∴△DAB为等腰直角三角形。
∴DO⊥AB。
∵PD为⊙O的切线,∴OD⊥PD。
∴DP∥AB。
(2)在Rt△ACB中,
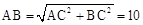 ,
,∵△DAB为等腰直角三角形,∴
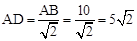 。
。∵AE⊥CD,∴△ACE为等腰直角三角形。∴
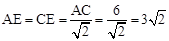 。
。在Rt△AED中,
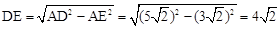 ,
,∴
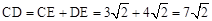 。
。∵AB∥PD,∴∠PDA=∠DAB=45°。∴∠PAD=∠PCD。
又∵∠DPA=∠CPD,∴△PDA∽△PCD。∴
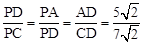 。
。∴PA=
 PD,PC=
PD,PC=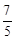 PD。
PD。又∵PC=PA+AC,∴
 PD+6=
PD+6=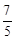 PD,解得PD=
PD,解得PD= 。
。试题分析:(1)连接OD,由AB为⊙O的直径,根据圆周角定理得∠ACB=90°,再由∠ACD=∠BCD=45°,则∠DAB=∠ABD=45°,所以△DAB为等腰直角三角形,所以DO⊥AB,根据切线的性质得OD⊥PD,于是可得到DP∥AB。
(2)先根据勾股定理计算出AB=10,由于△DAB为等腰直角三角形,可得到
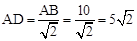 ;由△ACE为等腰直角三角形,得到
;由△ACE为等腰直角三角形,得到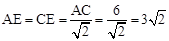 ,在Rt△AED中利用勾股定理计算出DE=
,在Rt△AED中利用勾股定理计算出DE=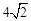 ,则CD=
,则CD=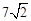 ,易证得∴△PDA∽△PCD,得到
,易证得∴△PDA∽△PCD,得到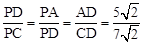 ,所以PA=
,所以PA= PD,PC=
PD,PC=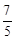 PD,然后利用PC=PA+AC可计算出PD。
PD,然后利用PC=PA+AC可计算出PD。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

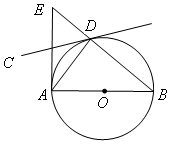
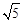 ,BD=2,求线段AE的长。
,BD=2,求线段AE的长。




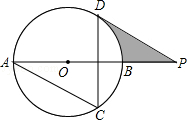

 cm,则弦AB 的长为
cm,则弦AB 的长为
 cm
cm cm
cm ,tan∠ABC=
,tan∠ABC= ,则CQ的最大值是
,则CQ的最大值是


