题目内容
如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.

(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.

(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=1,求⊙O的半径及sin∠ACE的值.
解:(1)证明:连接CD,
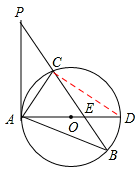
∵AD是⊙O的直径,∴∠ACD=90°。
∴∠CAD+∠ADC=90°。
又∵∠PAC=∠PBA,∠ADC=∠PBA,
∴∠PAC=∠ADC。∴∠CAD+∠PAC=90°。
∴PA⊥OA。
又∵AD是⊙O的直径,∴PA是⊙O的切线。
(2)由(1)知,PA⊥AD,
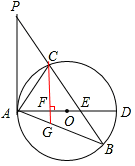
又∵CF⊥AD,∴CF∥PA。∴∠GCA=∠PAC。
又∵∠PAC=∠PBA,∴∠GCA=∠PBA。
又∵∠CAG=∠BAC,∴△CAG∽△BAC。
∴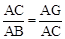 ,即AC2=AG•AB。
,即AC2=AG•AB。
∵AG•AB=12,∴AC2=12。∴AC=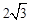 。
。
(3)设AF=x,
∵AF:FD=1:2,∴FD=2x。∴AD=AF+FD=3x。
在Rt△ACD中,∵CF⊥AD,∴AC2=AF•AD,即3x2=12。
解得;x=2。
∴AF=2,AD=6。∴⊙O半径为3。
在Rt△AFG中,∵AF=2,GF=1,
∴根据勾股定理得: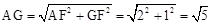 。
。
由(2)知,AG•AB=12,∴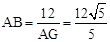 。
。
连接BD,
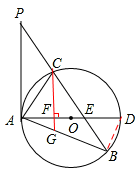
∵AD是⊙O的直径,∴∠ABD=90°。
在Rt△ABD中,∵sin∠ADB=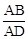 ,AD=6,
,AD=6,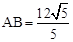 ∴sin∠ADB=
∴sin∠ADB=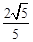 。
。
∵∠ACE=∠ACB=∠ADB,∴sin∠ACE=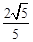 。
。

∵AD是⊙O的直径,∴∠ACD=90°。
∴∠CAD+∠ADC=90°。
又∵∠PAC=∠PBA,∠ADC=∠PBA,
∴∠PAC=∠ADC。∴∠CAD+∠PAC=90°。
∴PA⊥OA。
又∵AD是⊙O的直径,∴PA是⊙O的切线。
(2)由(1)知,PA⊥AD,

又∵CF⊥AD,∴CF∥PA。∴∠GCA=∠PAC。
又∵∠PAC=∠PBA,∴∠GCA=∠PBA。
又∵∠CAG=∠BAC,∴△CAG∽△BAC。
∴
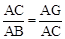 ,即AC2=AG•AB。
,即AC2=AG•AB。∵AG•AB=12,∴AC2=12。∴AC=
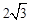 。
。(3)设AF=x,
∵AF:FD=1:2,∴FD=2x。∴AD=AF+FD=3x。
在Rt△ACD中,∵CF⊥AD,∴AC2=AF•AD,即3x2=12。
解得;x=2。
∴AF=2,AD=6。∴⊙O半径为3。
在Rt△AFG中,∵AF=2,GF=1,
∴根据勾股定理得:
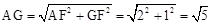 。
。由(2)知,AG•AB=12,∴
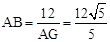 。
。连接BD,

∵AD是⊙O的直径,∴∠ABD=90°。
在Rt△ABD中,∵sin∠ADB=
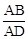 ,AD=6,
,AD=6,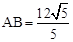 ∴sin∠ADB=
∴sin∠ADB=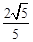 。
。∵∠ACE=∠ACB=∠ADB,∴sin∠ACE=
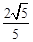 。
。试题分析:(1)根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案。
(2)首先得出△CAG∽△BAC,进而得出AC2=AG•AB,求出AC即可;
(3)先求出AF的长,根据勾股定理得
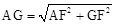 即可得出sin∠ADB=
即可得出sin∠ADB=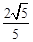 ,利用∠ACE=∠ACB=∠ADB,求出即可。
,利用∠ACE=∠ACB=∠ADB,求出即可。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 cm
cm  cm
cm  cm
cm 
 上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB.
上一点,连结AE,BE,BE交AC于点F,且AE2=EF•EB.
 ,求⊙O的半径.
,求⊙O的半径.


 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 cm.
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 cm.