题目内容
如图，AB为⊙O的直径，AC、DC为弦，∠ACD=60°，P为AB延长线上的点，∠APD=30°．
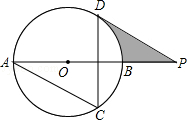
（1）求证：DP是⊙O的切线；
（2）若⊙O的半径为3cm，求图中阴影部分的面积．
（1）求证：DP是⊙O的切线；
（2）若⊙O的半径为3cm，求图中阴影部分的面积．
解：（1）证明：连接OD，
∵∠ACD=60°，
∴由圆周角定理得：∠AOD=2∠ACD=120°。
∴∠DOP=180°﹣120°=60°。
∵∠APD=30°，∴∠ODP=180°﹣30°﹣60°=90°。
∴OD⊥DP。
∵OD为半径，∴DP是⊙O切线。
（2）∵∠ODP=90°，∠P=30°，OD=3cm，
∴OP=6cm，由勾股定理得：DP=3
cm。
∴图中阴影部分的面积
。
∵∠ACD=60°，
∴由圆周角定理得：∠AOD=2∠ACD=120°。
∴∠DOP=180°﹣120°=60°。
∵∠APD=30°，∴∠ODP=180°﹣30°﹣60°=90°。
∴OD⊥DP。
∵OD为半径，∴DP是⊙O切线。
（2）∵∠ODP=90°，∠P=30°，OD=3cm，
∴OP=6cm，由勾股定理得：DP=3
cm。∴图中阴影部分的面积
。（1）连接OD，求出∠AOD，求出∠DOB，求出∠ODP，根据切线判定推出即可。
（2）求出OP、DP长，分别求出扇形DOB和△ODP面积，即可求出答案。
（2）求出OP、DP长，分别求出扇形DOB和△ODP面积，即可求出答案。
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
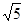
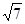
上一点，连结AE，BE，BE交AC于点F，且AE2=EF•EB．
，求⊙O的半径．
