Question

如图，在平面直角坐标系xOy中，一动直线l从y轴出发，以每秒1个单位长度的速度沿x轴向右平移，直线l与直线y=x相交于点P，以OP为半径的⊙P与x轴正半轴交于点A，与y轴正半轴交于点B．设直线l的运动时间为t秒．

（1）填空：当t=1时，⊙P的半径为       ，OA=       ，OB=       ；
（2）若点C是坐标平面内一点，且以点O、P、C、B为顶点的四边形为平行四边形．
①请你直接写出所有符合条件的点C的坐标；（用含t的代数式表示）
②当点C在直线y=x上方时，过A、B、C三点的⊙Q与y轴的另一个交点为点D，连接DC、DA，试判断△DAC的形状，并说明理由．

Answer 1

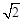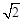解：（1）；2；2。
（2）①符合条件的点C有3个，分别为C₁（t，3t）、C₂（－t，t）、C₃（t，－t）。
②△DAC是等腰直角三角形。理由见解析

试题分析：（1）利用垂径定理、等腰直角三角形的性质求解。
（2）①本问关键是画出符合条件的图形，总共有3种情况，符合条件的点C有3个，如图1，

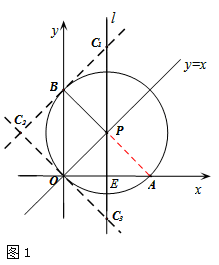
连接PA，
∵∠AOB=90°，由圆周角定理可知，AB为圆的直径，点A、P、B共线。
∵圆心P在直线y=x上，∴∠POA=∠POB=45°。
又∵PO=PA=PB，∴△POB与△POA均为等腰直角三角形。
设动直线l与x轴交于点E，
则有E（t，0），P（t，t），B（0，2t）。
∵OBPC₁为平行四边形，∴C₁P=OB=2t，C₁E=C₁P+PE=2t+t=3t，
∴C₁（t，3t）。
同理可求得：C₃（t，－t）。
∵OPBC₂为平行四边形，且PB=PO，∠OPB=90°，
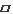∴OPBC₂为正方形，其对角线OB位于y轴上，则点P与点C₂关于x轴对称。
∴C₂（－t，t）。
∴符合条件的点C有3个，分别为C₁（t，3t）、C₂（－t，t）、C₃（t，－t）。
②正确作出图形，找到线段CD与AD之间的关联，这就是Rt△DCE∽Rt△ADO，通过计算可知其相似比为1，即两个三角形全等，从而得到CD=AD，△DAC为等腰直角三角形。本问符合条件的点C有2个，因此存在两种情形，分别如答图2和答图3所示。
△DAC是等腰直角三角形。理由如下：
当点C在第一象限时，如图2，连接DA、DC、PA、AC，

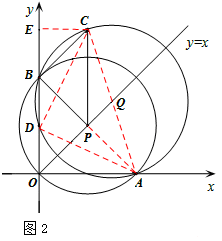
由（2）可知，点C的坐标为（t，3t），
由点P坐标为（t，t），点A坐标为（2t，0），点B坐标为（0，2t），可知OA=OB=2t，△OAB是等腰直角三角形。
又PO=PB，进而可得△OPB也是等腰直角三角形，
则∠POB=∠PBO=45°。
∵∠AOB=90°，∴AB为⊙P的直径。
∴A、P、B三点共线。
又∵BC∥OP，∴∠CBE=∠POB=45°。
∴∠ABC=180°－∠CBE－∠PBO=90°。∴AC为⊙Q的直径。∴DA⊥DC。
∴∠CDE+∠ADO=90°。
过点C作CE⊥y轴于点E，则有∠DCE+∠CDE=90°，∴∠ADO=∠DCE。
∴Rt△DCE∽Rt△ADO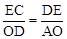，∴，即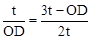，解得OD=t或OD=2t。
依题意，点D与点B不重合，∴舍去OD=2t，只取OD=t。
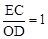∴，即相似比为1，此时两个三角形全等，则DC=AD。
∴△DAC是等腰直角三角形。
当点C在第二象限时，如图3，同上可证△DAC也是等腰直角三角形。

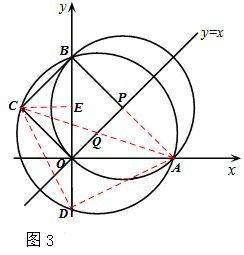
综上所述，当点C在直线y=x上方时，△DAC必为等腰直角三角形。