题目内容
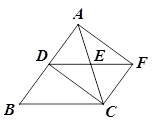
(1)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.

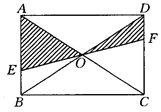
(2)如图,AC是⊙O的直径,弦BD交AC于点E。
①求证:⊿ADE∽⊿BCE;
②如果AD2=AE·AC,求证:CD=CB

求证:四边形BECF是平行四边形.

(2)如图,AC是⊙O的直径,弦BD交AC于点E。
①求证:⊿ADE∽⊿BCE;
②如果AD2=AE·AC,求证:CD=CB

1.证明见解析;2.(1)证明见解析;(2)证明见解析.
试题分析:(1)通过全等三角形(△AEB≌△DFC)的对应边相等证得BE=CF,由“在同一平面内,同垂直于同一条直线的两条直线相互平行”证得BE∥CF.则四边形BECF是平行四边形.
(2)(1)由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠B,又由对顶角相等,可证得:△ADE∽△BCE;
(2)由AD2=AE•AC,可得
 ,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,以求得AC⊥BD,由垂径定理即可证得CD=CB.
,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,以求得AC⊥BD,由垂径定理即可证得CD=CB.试题解析:(1)∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,
∴∠A=∠D,
在△AEB与△DFC中,
 ,
,∴△AEB≌△DFC(ASA),
∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
(2)(1)如图,

∵∠A与∠B是
 对的圆周角,
对的圆周角,∴∠A=∠B,
又∵∠1=∠2,
∴△ADE∽△BCE;
(2)如图,

∵AD2=AE•AC,
∴
 ,
,又∵∠A=∠A,
∴△ADE∽△ACD,
∴∠AED=∠ADC,
又∵AC是⊙O的直径,
∴∠ADC=90°,
即∠AED=90°,
∴直径AC⊥BD,
∴
 ,
,∴CD=CB.

练习册系列答案
相关题目

 .
.





 .
.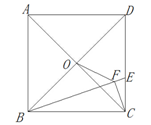
 中,
中, 是四边形内任意一点,
是四边形内任意一点,  ,
, ,
, ,
, 的面积分别为
的面积分别为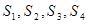 ,则一定成立的是 ( )
,则一定成立的是 ( )