��Ŀ����
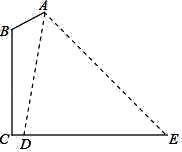
����Ŀ����֪����ͼ���߶�AB������BM���ڵ�B��

��1�����ó߹����������ͼ����������ͼ�ۼ�����д������
��������BM����һ��C��ʹAC��AB������AC
������ABM�Ľ�ƽ���߽�AC�ڵ�D
��������CM����һ��E��ʹCE��CD������DE
��2���ڣ�1����������ͼ���У�ͨ���۲�Ͳ������Է���BD��DE���뽫�����֤�����̲�������֤������AC��AB��
����� �������� ��
��BDƽ�֡�ABM��
���DBE����![]() ���� ��
���� ��
��CE��CD
���CDE����CED
���ACB����CDE+��CED��
���CED��![]() ��ACB
��ACB
���DBE����CED��
��BD��DE������ ������
���𰸡���1��ͼ�μ���������2��ABC��ACB��ABC���ȽǶԵȱߣ�
��������
��1�����ճ߹���ͼ�IJ�����ͼ���ɣ�
��2�����ݵ��������ε����ʼ���ƽ���ߵĶ���֤������.
�⣺��1��ͼ����ͼ��ʾ��
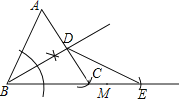
��2����AC��AB��
���ABC����ACB��
��BDƽ�֡�ABM��
���DBE��![]() ��ABC
��ABC
��CE��CD
���CDE����CED
���ACB����CDE+��CED��
���CED��![]() ��ACB
��ACB
���DBE����CED��
��BD��DE�����ȽǶԵȱߣ���
�ʴ�Ϊ��ABC��ACB��ABC���ȽǶԵȱߣ�

��ϰ��ϵ�д�
�����Ŀ