Question

【题目】“五一”期间，甲、乙两家商店以同样价格销售相同的商品，两家优惠方案分别为：甲店一次性购物中超过200元后的价格部分打七折；乙店一次性购物中超过500元后的价格部分打五折，设商品原价为x元（x≥0），购物应付金额为y元．

（1）求在甲商店购物时y与x之间的函数关系；

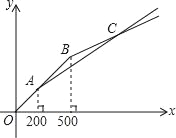
（2）两种购物方式对应的函数图象如图所示，求交点C的坐标；

（3）根据图象，请直接写出“五一”期间选择哪家商店购物更优惠．

Answer 1

【答案】（1）当0≤x≤200时，y1=x，当x＞200时，y1=0.7x+60；（2）点C坐标（950，725）；（3）见解析.

【解析】

（1）根据题意分当0≤x≤200时，当x>200时两种情况分别求出y1即可.

（2）求出直线BC，列方程组即可解决问题.

（3）利用图象即可解决问题.

解：（1）根据题意，得

当0 ≤ x ≤ 200时，y1＝x；

当x ＞ 200时，y1＝200＋0.7（x－ 200）

＝0.7 x＋60．

综上所知，甲商店购物时y1与x之间的函数关系式为

y1＝﹛x（0 ≤ x ≤ 200）；0.7 x＋60（x ＞ 200）．

（2）由图象可知，交点C的横坐标大于500，

当x﹥500时，设乙商店购物时应付金额为y2元，

则y2＝500＋0.5（x－ 500）＝0.5 x＋250．

由（1）知，当x﹥500时，y1＝0.7 x＋60．

由于点C是y1与y2的交点，

∴令0.7 x＋60＝0.5 x＋250．

解得x＝950，此时y1＝y2＝725．

即交点C的坐标为（950，725）．

（3）结合图像和（2）可知：

当0 ≤ x ≤ 200或x＝950时，

选择甲、乙两家商店购物费用相同；

当200＜x＜950时，选择甲商店购物更优惠；

当x﹥950时，选择乙商店购物更优惠．

“点睛”本题考查一次函数的应用，方程组等知识，解题是关键是学会构建一次函数，知道利用方程组求两个和尚图象交点坐标，学会利用图象比较函数值大小，属于中考常考题型.