ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥єЂЋЊњ™ЈҐЅЋ“ї÷÷–¬–ЌµƒЉ“µз≤ъ∆Ј£ђ”÷ Јк°∞Љ“µзѕ¬ѕз°±µƒ”≈їЁ’ю≤я£Ѓѕ÷Ќґ„ ![]() Ќт‘™”√”ЏЄ√≤ъ∆ЈµƒєгЄжіўѕъ£ђ“—÷™Є√≤ъ∆Јµƒ±ЊµЎѕъ џЅњ
Ќт‘™”√”ЏЄ√≤ъ∆ЈµƒєгЄжіўѕъ£ђ“—÷™Є√≤ъ∆Јµƒ±ЊµЎѕъ џЅњ![]() £®Ќтћ®£©”л±ЊµЎµƒєгЄжЈ—”√
£®Ќтћ®£©”л±ЊµЎµƒєгЄжЈ—”√![]() £®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµ¬ъ„г
£®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµ¬ъ„г![]() £ЃЄ√≤ъ∆ЈµƒЌвµЎѕъ џЅњ
£ЃЄ√≤ъ∆ЈµƒЌвµЎѕъ џЅњ![]() £®Ќтћ®£©”лЌвµЎєгЄжЈ—”√
£®Ќтћ®£©”лЌвµЎєгЄжЈ—”√![]() £®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµњ…”√»зЌЉЋщ Њµƒ≈„ќпѕяЇЌѕяґќ
£®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµњ…”√»зЌЉЋщ Њµƒ≈„ќпѕяЇЌѕяґќ![]() јі±н Њ£Ѓ
јі±н Њ£Ѓ
∆д÷–µг![]() ќ™≈„ќпѕяµƒґ•µг£Ѓ
ќ™≈„ќпѕяµƒґ•µг£Ѓ
![]() љбЇѕЌЉѕу£ђ«у≥ц
љбЇѕЌЉѕу£ђ«у≥ц![]() £®Ќтћ®£©”лЌвµЎєгЄжЈ—”√
£®Ќтћ®£©”лЌвµЎєгЄжЈ—”√![]() £®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љ£ї
£®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љ£ї
![]() «уЄ√≤ъ∆Јµƒѕъ џ„№Ѕњ
«уЄ√≤ъ∆Јµƒѕъ џ„№Ѕњ![]() £®Ќтћ®£©”л±ЊµЎєгЄжЈ—”√
£®Ќтћ®£©”л±ЊµЎєгЄжЈ—”√![]() £®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љ£ї
£®Ќт‘™£©÷ЃЉдµƒЇѓ эєЎѕµ љ£ї
![]() »зЇќ∞≤≈≈єгЄжЈ—”√≤≈ƒ№ єѕъ џ„№Ѕњ„оіу£њ
»зЇќ∞≤≈≈єгЄжЈ—”√≤≈ƒ№ єѕъ џ„№Ѕњ„оіу£њ
°Њір∞Є°њ![]() µ±
µ±![]() ±£ђ
±£ђ![]() £їµ±
£їµ±![]() ±£ђ
±£ђ![]() £ї
£ї![]() Љыљвќц£ї
Љыљвќц£ї![]() ±ЊµЎєгЄжЈ—”√ќ™15Ќт‘™£ђЌвµЎєгЄжЈ—”√ќ™25Ќт‘™.
±ЊµЎєгЄжЈ—”√ќ™15Ќт‘™£ђЌвµЎєгЄжЈ—”√ќ™25Ќт‘™.
°Њљвќц°њ
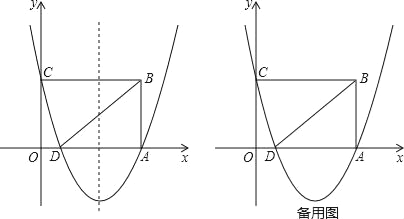
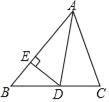
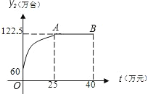
£®1£©Ј÷ґќ«уљв£ђµ±0°№t°№25 ±£ђ“—÷™ґ•µгA„ш±к£ђ…иґ•µг љљвќц љ£ђіъ»л“—÷™µг£®0,60£©Љіњ…«уљв£їµ±25£Љt°№40 ±£ђy=122.5£ї
£®2£©”…ћв“вњ…µ√t=40-x£ђЄщЊЁtµƒ»°÷µЈґќІњ…»Јґ®xµƒ»°÷µЈґќІќ™0°№x£Љ15°Ґ15°№x£Љ25°Ґ25°№x°№40£ђ‘тy=y1+y2£ђ∞і’’xµƒЈґќІЈ÷±р«уљв.
£®3£©”……ѕ цЋщ«у±ніп љЈ÷±рЉ∆Ћг√њґќЇѓ эµƒ„оіу÷µ£ђ‘ў»°»эЄц э÷µ÷–µƒ„оіу÷µЉіњ….
![]() ”…Їѓ эЌЉѕуњ…÷™£ђ
”…Їѓ эЌЉѕуњ…÷™£ђ
µ±![]() ±£ђЇѓ эЌЉѕуќ™≈„ќпѕяµƒ“ї≤њЈ÷£ђ
±£ђЇѓ эЌЉѕуќ™≈„ќпѕяµƒ“ї≤њЈ÷£ђ
…иљвќц љќ™![]() £ђ
£ђ
∞—![]() іъ»лљвќц љµ√£ђ
іъ»лљвќц љµ√£ђ
![]() £ї
£ї
µ±![]() ±£ђ
±£ђ
![]() £ї
£ї
![]() ”…ћв“вњ…µ√t=40-x£ђЄщЊЁtµƒ»°÷µЈґќІµ√£Ї
”…ћв“вњ…µ√t=40-x£ђЄщЊЁtµƒ»°÷µЈґќІµ√£Ї
![]() ±£ђ
±£ђ![]() £ї
£ї
![]() ±£ђ
±£ђ![]() £ї
£ї
![]() ±£ђ
±£ђ![]()
![]() £Ѓ
£Ѓ
![]() ±£ђ„оіуy=3°Ѕ15+122.5=167.5£ђ
±£ђ„оіуy=3°Ѕ15+122.5=167.5£ђ
![]() ±£ђ„оіуy=-0.1°Ѕ625+122.5=60£ђ
±£ђ„оіуy=-0.1°Ѕ625+122.5=60£ђ
![]() ±£ђ„оіуy=-0.1°Ѕ625+125=62.5£ђ
±£ђ„оіуy=-0.1°Ѕ625+125=62.5£ђ
є µ±x=15 ±£ђy÷µ„оіу£ђ
є £ђ±ЊµЎєгЄжЈ—”√ќ™15Ќт‘™£ђЌвµЎєгЄжЈ—”√ќ™25Ќт‘™.

 √ы–£њќћ√ѕµЅ–ір∞Є
√ы–£њќћ√ѕµЅ–ір∞Є