题目内容
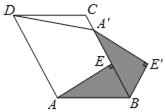
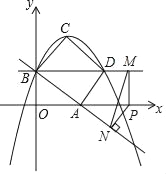
【题目】(题文)如图,在平面直角坐标系中,直线y=﹣x+2与坐标轴分别交于A,B两点,过点B作BD∥x轴,抛物线y=﹣![]() x2+bx+c经过B,D两点,且对称轴为x=2,设x轴上一动点P(n,0),过点P分别作直线BD,AB的垂线,垂足分别为M,N.
x2+bx+c经过B,D两点,且对称轴为x=2,设x轴上一动点P(n,0),过点P分别作直线BD,AB的垂线,垂足分别为M,N.
(1)求抛物线的解析式及顶点C的坐标;
(2)设四边形ABCD的面积为S四边形ABCD,当n为何值时,![]() =
=![]() ;
;
(3)是否存在点P(n,0),使得△PMN为等腰三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+2x+2,(2,4);(2)当n=﹣2或n=6时,
x2+2x+2,(2,4);(2)当n=﹣2或n=6时,![]() =
=![]() ;(3)存在P(﹣2,0)
;(3)存在P(﹣2,0)
【解析】
(1)根据对称轴公式以及点![]() 坐标,构建方程组即可解决问题;
坐标,构建方程组即可解决问题;
(2)分两种情形分别构建方程即可解决问题;
(3)分三种情形:①![]() ,②
,②![]() ,③
,③![]() ,分别求解解决问题.
,分别求解解决问题.
(1)当x=0时,直线y=﹣x+2=2,即B(0,2)
当y=0时,﹣x+2=0,解得x=2,即A(2,0),
将B点坐标代入函数解析式,对称轴,得
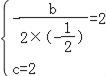 ,
,
解得![]() ,
,
抛物线的解析式为y=﹣![]() x2+2x+2,
x2+2x+2,
当x=2时,y=﹣![]() ×22+2×2+2=4,
×22+2×2+2=4,
顶点坐标(2,4);
(2)如图1,过N作NH⊥x轴于H,
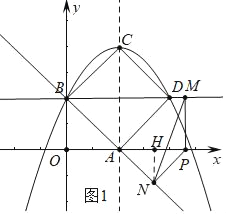
∵BD∥x轴,抛物线的对称轴x=2,连接AC,则AC⊥BD,
∴S四边形ABCD=![]() ×4×4=8,
×4×4=8,
∵![]() =
=![]() ,
,
∴S△PMN=2,又∵N在直线y=﹣x+2上,
∴∠NPH=45°,且S△PMN=![]() PHPM,
PHPM,
∵BD∥x轴,
∴PM=2,当点P在A点右侧时,2+PH=n,即PH=![]() ,
,
∴S△PMN=![]() PHPM=
PHPM=![]() ×
×![]() ×2=2解得n=6;
×2=2解得n=6;
当点P在A点左侧时,2﹣PH=n,即PH=![]() ,
,
∴S△PMN=![]() PHPM=
PHPM=![]() ×
×![]() ×2=2,解得n=﹣2,
×2=2,解得n=﹣2,
综上所述,当n=﹣2或n=6时,![]() =
=![]() ;
;
(3)存在.①如图 2,当PM=PN时,
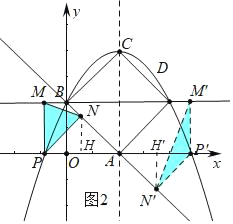
∵PN=PM=2,PH=![]() ,n=2
,n=2![]() ,
,
∴p(2+2![]() ,0)或P(2﹣2
,0)或P(2﹣2![]() ,0);
,0);
②如图3,当MN=PN时,
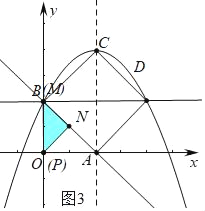
∵MN⊥PN,
∴△PMN是等腰直角三角形,且PM=2,
∴PN=![]() ,
,
∴P(0,0);
③当PM=MN时,
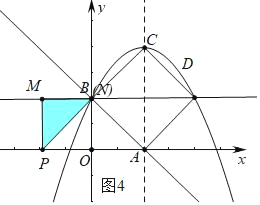
∵MN=PM=2,MN⊥PM,
∴△PMN是等腰直角三角形,
∴MB=2,∴P(﹣2,0).

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案