题目内容
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=5,AB=1,点P是线段BC (不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

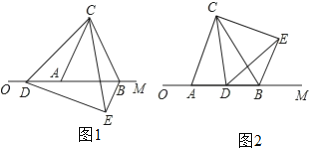
(1)如图1,当BP= 时,△ADP是等腰直角三角形.(请直接写出答案)
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并加以证明.
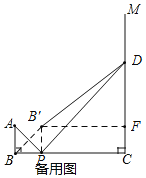
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,请画出图形,并求线段B′D的长度.(参考定理:若直角△ABC中,∠C是直角,则BC2+AC2=AB2)
【答案】(1)4;
(2)PB和PC的数量关系:PB=PC,证明见解析;
(3)线段B′D的长度为5.
【解析】
(1)若△ADP是等腰直角三角形.则AP=DP,必须要求△APB≌△PDC,则![]() ,所以BP=4;
,所以BP=4;
(2)延长线段AP、DC交于点E,则△DPA≌△DPE,PA=PE,进一步可证明△APB≌△EPC,则PB=PC;
(3)先按要求作出图形,然后将B′D放在直角三角形中,利用勾股定理求出B′D的长度.
解:(1)当BP=4时,CP=BC﹣BP=5=4=1,
∵AB=1,
∴AB=PC,
∵AB⊥BC,DP⊥AP,CM⊥BC,
∴∠B=∠C=90°,∠APB+∠DPC=90°=∠PDC+∠DPC,
∴∠APB=∠PDC,
在△APB和△PDC中,
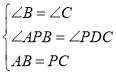
∴△APB≌△PDC(AAS),
∴AP=DP,
又∵∠APD=90°,
∴△ADP是等腰直角三角形,
故答案为:4;
(2)PB和PC的数量关系:PB=PC,
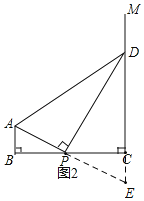
证明:如图2,延长线段AP、DC交于点E,
∵DP平分∠ADC,
∴∠ADP=∠EDP.
∵DP⊥AP,
∴∠DPA=∠DPE=90°.
在△DPA和△DPE中,

∴△DPA≌△DPE(ASA),
∴PA=PE.
∵AB⊥BP,CM⊥CP,
∴∠ABP=∠ECP=90°.
在△APB和△EPC中,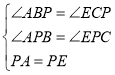
∴△APB≌△EPC(AAS),
∴PB=PC;
(3)如图,连接B'P,过点B'作B'F⊥CD于F,则∠B'FC=∠C=90°,
∵△PDC是等腰三角形,
∴△PCD为等腰直角三角形,即∠DPC=45°,
又∵DP⊥AP,
∴∠APB=45°,
∵点B关于AP的对称点为点B′,
∴∠BPB'=90°,∠APB=45°,BP=B'P,
∴△ABP为等腰直角三角形,四边形B'PCF是矩形,
∴BP=AB=1=B'P,PC=5=1=4=B'F,CF=B'P=1,
∴B'F=4,DF=4﹣1=3,
∴Rt△B'FD中,B'D=![]() =5,
=5,
故线段B′D的长度为5.