题目内容
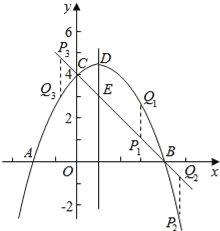
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若直线BC的函数解析式为y’=kx+b,求当满足y<y’时,自变量x的取值范围.
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.

【答案】(1)抛物线的解析式为y=![]() ;
;
(2)x<0 或x>4时,y<y’;
(3)P1(3,1),P2(![]() ,
, ![]() )P3(
)P3(![]() ,
, ![]() )
)
【解析】试题分析:(1)先把C(0,4)代入y=ax2+bx+c,得出c=4①,再由抛物线的对称轴x=-![]() =1,得到b=-2a②,抛物线过点A(-2,0),得到0=4a-2b+c③,然后由①②③可解得,a=-
=1,得到b=-2a②,抛物线过点A(-2,0),得到0=4a-2b+c③,然后由①②③可解得,a=-![]() ,b=1,c=4,即可求出抛物线的解析式为y=-
,b=1,c=4,即可求出抛物线的解析式为y=-![]() x2+x+4;
x2+x+4;
(2)先求出点B的坐标再观察图象,y时对应的图象为直线在上抛物线在下方的部分,即可得到x的取值范围;
(3)因为PQ∥DE,所以只需PQ=AC即可,求出PQ的参数长度便可列式求解.
试题解析:(1)∵抛物线y=ax2+bx+c(a≠0)过点C(0,4),
∴c=4 ①.
∵对称轴x=-![]() =1,
=1,
∴b=-2a ②.
∵抛物线过点A(-2,0),
∴0=4a-2b+c ③,
由①②③解得,a=-![]() ,b=1,c=4,
,b=1,c=4,
∴抛物线的解析式为y=-![]() x2+x+4;
x2+x+4;
(2)∵A(﹣2,0),对称轴x=1,
∴B(4,0)
根据图像,得x<0 或x>4时,y
(3)已知DE∥PQ,当DE=PQ时,以D、E、P、Q为顶点的四边形是平行四边形,
设点F的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣ ![]() m2+m+4),
m2+m+4),
∴|﹣m+4+![]() m2﹣m﹣4|=DE=
m2﹣m﹣4|=DE=![]() ,
,
∴m=1,m=3,m=![]() ,m=
,m=![]()
当m=1时,线段PQ与DE重合,舍去.
∴P1(3,1),
P2(![]() ,
, ![]() ),
),
P3(![]() ,
, ![]() ).
).

 阅读快车系列答案
阅读快车系列答案