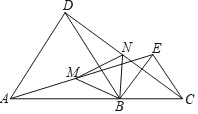
题目内容
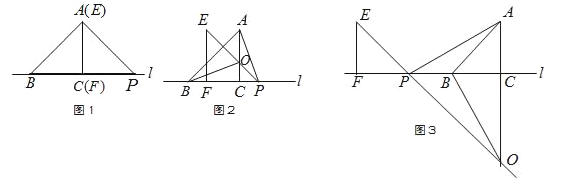
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)如图1,请你写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.猜想并写出BO与AP所满足的数量关系和位置关系,并说明理由;
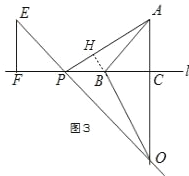
(3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明理由.
【答案】(1)AP=AB,AP⊥AB;(2)AP=BO,AP⊥BO;(3)AP=BO,AP⊥BO.
【解析】整体分析:
(1)根据△ABC与△EFP是全等的等腰直角三角形,判断△ABP是等腰直角三角形;(2)用SAS证明△ACP≌△BCO得到AP=BO,∠CAP=∠CBO,结合三角形的内角和可得BO⊥AP;(3)结合与理由和(2)类似.
解:(1)∵AC⊥BC,且AC=BC,边EF与边AC重合,且EF=FP.
∴△ABC与△EFP是全等的等腰直角三角形,
∴∠BAC=∠CAP=45°,AB=AP,
∴∠BAP=90°,
∴AP=AB,AP⊥AB;
(2)AP=BO,AP⊥BO.理由如下:
延长BO交AP于H点,如图2
∵∠EPF=45°,
∴△OPC为等腰直角三角形,
∴OC=PC,
∵在△ACP和△BCO中
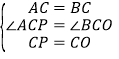
∴△ACP≌△BCO(SAS),
∴AP=BO,∠CAP=∠CBO,
又∵∠AOH=∠BOC,
∴∠AHO=∠BCO=90°,
∴AP⊥BO,
即BO与AP所满足的数量关系为相等,位置关系为垂直;

(3)BO与AP所满足AP=BO,AP⊥BO.理由如下:
延长OB交AP于点H,如图3,
∵∠EPF=45°,
∴∠CPO=45°,
∴△CPO为等腰直角三角形,
∴OC=PC,
∵在△APC和△OBC中,
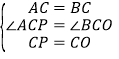
∴△APC≌△BOC(SAS),
∴AP=BO,∠APC=∠COB,
而∠PBH=∠CBO,
∴∠PHB=∠BCO=90°,
∴BO⊥AP,
即BO与AP所满足的数量关系为相等,位置关系为垂直.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案