题目内容
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣3,0)、B(1,0)两点,与y轴交于点C,D是抛物线的顶点,E是对称轴与x轴的交点.
(1)求抛物线的解析式,并在﹣4≤x≤2范围内画出此抛物线的草图;
(2)若点F和点D关于x轴对称,点P是x轴上的一个动点,过点P作PQ∥OF交抛物线于点Q,是否存在以点O、F、P、Q为顶点的平行四边形?若存在,求出点P坐标;若不存在,请说明理由.

【答案】(1)见解析(2)P1(﹣2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(﹣2,0).
,0),P3(﹣2,0).
【解析】:试题分析:(1)将A(﹣3,0)、B(1,0)两点带入二次函数表达式,即可求得二次函数解析式,以及顶点D的坐标。进而画出在﹣4≤x≤2范围内此抛物线的草图,可运用描点法画。(2)若存在以点O、F、P、Q为顶点的平行四边形,则F、Q纵坐标的绝对值相等。点F 的坐标已知,可分情况讨论,求点Q坐标,从而求得P点坐标。
试题解析:解:(1)根据题意得: ![]() ,解得:
,解得: ![]() ,
,
∴解析式为y=﹣x2﹣2x+3.
当x=﹣![]() =﹣1时,y=4,
=﹣1时,y=4,
∴顶点D的坐标为(﹣1,4),
∴点F的坐标为(﹣1,﹣4).
此抛物线的草图如图所示
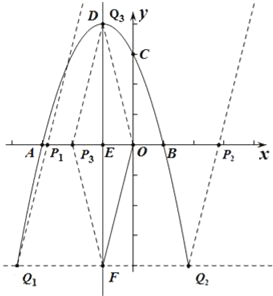
(2)若以O、F、P、Q为顶点的平行四边形存在,
则点Q(x,y)必须满足|y|=|EF|=4.
①当y=﹣4时,﹣x2﹣2x+3=﹣4,
解得,x=﹣1±2![]() ,
,
∴Q1(﹣1﹣2![]() ,﹣4),Q2(﹣1+2
,﹣4),Q2(﹣1+2![]() ,﹣4)
,﹣4)
∴P1(﹣2![]() ,0),P2(2
,0),P2(2![]() ,0).
,0).
②当y=4时,﹣x2﹣2x+3=4,
解得,x=﹣1,
∴Q3(﹣1,4),
∴P3(﹣2,0),
综上所述,符合条件的点有三个即:
P1(﹣2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(﹣2,0).
,0),P3(﹣2,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目