题目内容
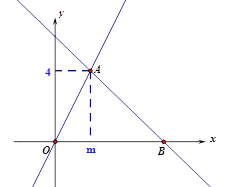
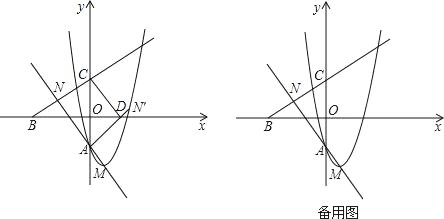
【题目】已知抛物线y=x2﹣2x+a(a<0)与y轴相交于点A,顶点为M.直线y=![]() x﹣a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
x﹣a分别与x轴,y轴相交于B,C两点,并且与直线AM相交于点N.
(1)试用含a的代数式分别表示点M与N的坐标;
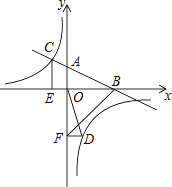
(2)如图,将△NAC沿y轴翻折,若点N的对应点N′恰好落在抛物线上,AN′与x轴交于点D,连接CD,求a的值和四边形ADCN的面积;
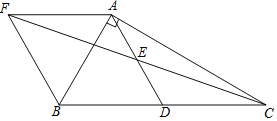
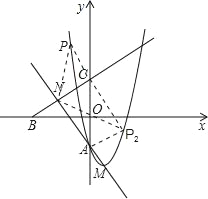
(3)在抛物线y=x2﹣2x+a(a<0)上是否存在一点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出P点的坐标;若不存在,试说明理由.
【答案】(1)M(1,a﹣1),N(![]() a,﹣
a,﹣![]() a);(2)a=
a);(2)a=![]() , S四边形ADCN
, S四边形ADCN![]() ;(3)详见解析.
;(3)详见解析.
【解析】分析:(1)、已知了抛物线的解析式,不难用公式法求出M的坐标为(1,a-1).由于抛物线过A点,因此A的坐标是(0,a).根据A,M的坐标,用待定系数法可得出直线AM的解析式.联立方程组即可求出N的坐标为;(2)、根据折叠的性质不难得出N与N′正好关于y轴对称,得出N′的坐标.由于N′在抛物线上,因此将N′的坐标代入抛物线的解析式中即可得出a的值.也就能确定N,C的坐标.求四边形ADCN的面积,可分成△ANC和△ADC两部分来求.已经求得了A,C,N的坐标,可求出AC的长以及N,D到y轴的距离.也就能求出△ANC和△ADC的面积,进而可求出四边形ADCN的面积;(3)、本题可分两种情况进行讨论:①当P在y轴左侧时,如果使以P,N,A,C为顶点的四边形为平行四边形,那么P需要满足的条件是PN平行且相等于AC,也就是说,如果N点向上平移AC个单位即-2a后得到的点就是P点.然后将此时P的坐标代入抛物线中,如果没有解说明不存在这样的点P,如果能求出a的值,那么即可求出此时P的坐标.②当P在y轴右侧时,P需要满足的条件是PN与AC应互相平分(平行四边形的对角线互相平分),那么NP必过原点,且关于原点对称.那么可得出此时P的坐标,然后代入抛物线的解析式中按①的方法求解即可.
详解:解:(1)M(1,a﹣1),N(![]() a,﹣
a,﹣![]() a);
a);
(2)∵由题意得点N与点N′关于y轴对称,∴N′(﹣![]() a,﹣
a,﹣![]() a).
a).
将N′的坐标代入y=x2﹣2x+a得:﹣![]() a=
a=![]() a2+
a2+![]() a+a,
a+a,
∴a1=0(不合题意,舍去),![]() .∴N(﹣3,
.∴N(﹣3, ![]() ),
),
∴点N到y轴的距离为3. ∵A(0,﹣![]() ),N′(3,
),N′(3, ![]() ),
),
∴直线AN′的解析式为![]() ,它与x轴的交点为D(
,它与x轴的交点为D(![]() ) ∴点D到y轴的距离为
) ∴点D到y轴的距离为![]() .
.
∴S四边形ADCN=S△ACN+S△ACD=![]() ;
;
(3)存在,理由如下:
①当点P在y轴的左侧时,若ACPN是平行四边形,则PN![]() AC,
AC,
则把N向上平移﹣2a个单位得到P,坐标为(![]() a,﹣
a,﹣![]() a),代入抛物线的解析式,
a),代入抛物线的解析式,
得:﹣![]() a=
a=![]() a2﹣
a2﹣![]() a+a, 解得a1=0(不舍题意,舍去),a2=﹣
a+a, 解得a1=0(不舍题意,舍去),a2=﹣![]() ,
,
则P(﹣![]() ,
, ![]() );
);
②当点P在y轴的右侧时,若APCN是平行四边形,则AC与PN互相平分,
则OA=OC,OP=ON. 则P与N关于原点对称, 则P(﹣![]() a,
a, ![]() a);
a);
将P点坐标代入抛物线解析式得: ![]() a=
a=![]() a2+
a2+![]() a+a, 解得a1=0(不合题意,舍去),a2=﹣
a+a, 解得a1=0(不合题意,舍去),a2=﹣![]() ,
,
则P(![]() ,﹣
,﹣![]() ).
).
故存在这样的点P(﹣![]() ,
, ![]() )或P(
)或P(![]() ,﹣
,﹣![]() ),能使得以P,A,C,N为顶点的四边形是平行四边形.
),能使得以P,A,C,N为顶点的四边形是平行四边形.

【题目】某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-4 | +8 | -9 | +8 | +6 | -5 | -2 |
(1)求收工时距A地多远?
(2)若每km耗油0.4升,问一天共耗油多少升?