题目内容
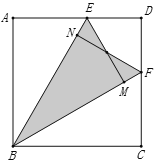
【题目】如图，正方形ABCD的边长为
，点E、F分别为边AD、CD上一点，将正方形分别沿BE、BF折叠，点A的对应点M恰好落在BF上，点C的对应点N恰好落在BE上，则图中阴影部分的面积为_________．
【答案】
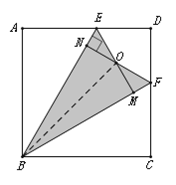
【解析】分析：设NE＝x，由对称的性质和勾股定理，用x分别表示出ON，OE，OM，在直角△OEN中用勾股定理列方程求x，则可求出△OBE的面积.
详解：连接BO.
∠ABE＝∠EBF＝∠FBC＝30°，AE＝1＝EM，BE＝2AE＝2.
∠BNF＝90°，∠NEO＝60°，∠EON＝30°，
设EN＝x，则EO＝2x，ON＝
x＝OM，
∴OE＋OM＝2x＋x＝(2＋)x＝1.∴x＝
＝2－.
∴ON＝x＝(2－)＝2－3.
∴S＝2S△BOE＝2×(
×BE×ON)＝2×[×2×(2－3)]＝4－6.
故答案为
.
练习册系列答案
走进文言文系列答案
相关题目
