题目内容
【题目】解不等式组: 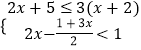 ,并写出它的非负整数解.
,并写出它的非负整数解.
【答案】解:解不等式①得:x≥﹣1, 解不等式②得:x≤3,
所以不等式组的解集为:﹣1≤x≤3,
所以不等式组的非负整数解为3,2,1,0.
【解析】分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可,再找出解集范围内的非负整数即可.
【考点精析】通过灵活运用一元一次不等式组的解法和一元一次不等式组的整数解,掌握解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 );使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解)即可以解答此题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】列一元一次方程解应用题:
2018年是我国改革开放40周年,改革开放是当代中国发展进步的必由之路,是实现中国梦的必由之路. 2018年10月20日在国家大剧院举行了《可爱的中国》庆祝改革开放40周年音乐会. 本次演出的票价分为以下几个类别,如下表所示:
演出票类别 | A类 | B类 | C类 | D类 | E类 |
演出票单价(元/张) | 300 | 280 | 240 | 180 | 100 |
小宇购买了A类和C类的演出票共10张,他发现这10张演出票的总价恰好可以购买8张B类票和4张E类票. 问小宇购买A类和C类的演出票各几张?