Question

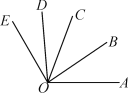
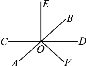
【题目】如图所示，直线AB，CD相交于点O，OE⊥CD于点O，OD平分∠BOF，∠BOE＝50°，求∠AOC、∠EOF与∠AOF的度数．

Answer 1

【答案】∠AOF＝100°.

【解析】由OE⊥CD，求出∠BOD＝90°－∠BOE＝40°.可得∠AOC＝∠BOD＝40°；

由OD平分∠BOF，得∠BOF＝2∠BOD.再得∠EOF＝∠EOB＋∠BOF，进一步得

∠AOF＝180°－∠BOF.

解：∵OE⊥CD，∴∠EOD＝90°，

∴∠BOD＝90°－∠BOE＝90°－50°＝40°.

∴∠AOC＝∠BOD＝40°.

∵OD平分∠BOF，

∴∠BOF＝2∠BOD＝2×40°＝80°.

∴∠EOF＝∠EOB＋∠BOF＝50°＋80°＝130°，

∠AOF＝180°－∠BOF＝180°－80°＝100°.