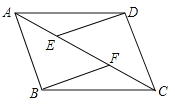
题目内容
【题目】如图,在![]() 中,
中, ![]() ,
,![]() ,
, ![]() 是由
是由![]() 绕点
绕点![]() 按顺时针方向旋转得到的,连接
按顺时针方向旋转得到的,连接![]() 、
、![]() 相交于点
相交于点![]() .
.
(1)求证: ![]() ;
;
(2)当四边形![]() 为菱形时,求
为菱形时,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CD;
(2)由菱形的性质得到DE=AE=AC=AB=1,AC∥DE,根据等腰三角形的性质得∠AEB=∠ABE,根据平行线得性质得∠ABE=∠BAC=45°,所以∠AEB=∠ABE=45°,于是可判断△ABE为等腰直角三角形,所以BE=![]() AC=
AC=![]() ,于是利用BD=BE-DE求解.
,于是利用BD=BE-DE求解.
试题解析:(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
(2)解:∵四边形ACDE为菱形,AB=AC=1,
∴DE=AE=AC=AB=1,AC∥DE,
∴∠AEB=∠ABE,∠ABE=∠BAC=45°,
∴∠AEB=∠ABE=45°,
∴△ABE为等腰直角三角形,
∴BE=![]() AC=
AC=![]() ,
,
∴BD=BE-DE=![]() -1.
-1.

【题目】2013年1月,由于雾霾天气持续笼罩我国中东部大部分地区,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如下表:
品名 | 甲种口罩 | 乙种口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种口罩各多少袋?
(2)该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?