题目内容
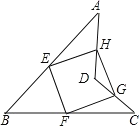
【题目】如图,E. F. G、H分别是边AB、BC、CD、DA的中点.
(1)判断四边形EFGH的形状,并说明你的理由;
(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形?证明你的理由.
【答案】(1)四边形EFGH是平行四边形,证明详见解析;(2)当BD=AC,且BD⊥AC时,EFGH是正方形,理由详见解析.
【解析】试题分析:(1)连接AC,由E、F、G、H分别是边AB、BC、CD、DA的中点,根据三角形中位线的性质,易得EF∥HG∥AC,且EF=HG=![]() AC,则可得四边形EFGH是平行四边形;
AC,则可得四边形EFGH是平行四边形;
(2)当BD=AC,易证得四边形ABCD是菱形,当BD⊥AC时,易得∠EHG=90°,则可得四边形EFGH是正方形.
试题解析:(1)四边形EFGH是平行四边形.
理由:连接AC,

∵E、F分别是AB、BC的中点,
∴EF∥AC,且EF=![]() AC,
AC,
同理,HG∥AC,且HG=![]() AC,
AC,
∴EF∥HG,且EF=HG,
∴四边形EFGH是平行四边形;
(2)当BD=AC,且BD⊥AC时,EFGH是正方形.
理由:连接AC,BD,

∵E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=GH=![]() AC,GH=FG=
AC,GH=FG=![]() BD,EH∥BD,GH∥AC,
BD,EH∥BD,GH∥AC,
∵BD=AC,BD⊥AC,
∴EH=EF=FG=GH,EH⊥GH,
∴四边形EFGH是菱形,∠EHG=90°,
∴四边形EFGH是正方形.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
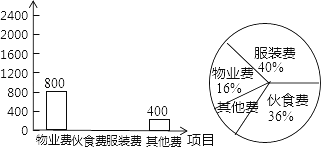
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | ________ | ________ | 400 |
(4)请将条形统计图补充完整.
【题目】某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.
x(元/件) | 35 | 40 | 45 | 50 | 55 |
y(件) | 550 | 500 | 450 | 400 | 350 |
(1)试求y与x之间的函数表达式;
(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价﹣成本总价);
(3)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?最大毛利润是多少?此时每天的销售量是多少?