题目内容
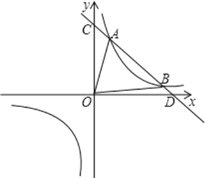
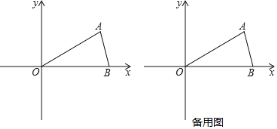
【题目】如图，平面直角坐标系中，点A是x轴负半轴上一个定点，点P是函数
上一个动点，
轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会
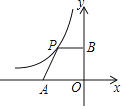
A. 先增后减 B. 先减后增 C. 逐渐减小 D. 逐渐增大
【答案】D
【解析】
过点P作PC⊥x轴于点C，根据k的几何意义可知矩形PBOC的面积为6，然后只需要讨论△APC的面积大小即可．
过点P作PC⊥x轴于点C，
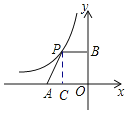
∵点P在y=-
（x＜0）
∴矩形PBOC的面积为6
设A的坐标为（a，0），P坐标（x，）（x＜0），
△APC的面积为S，
当a＜x＜0时，
∴AC=x-a，
∴PC=-
∴△APC的面积为S=
（x-a）
=-3（1-
）
∵a＜0，
∴-a＞0，
∴-在a＜x＜0上随着x的增大而减小，
∴1-在a＜x＜0上随着x的增大而减小，
∴-3（1-）在a＜x＜0上随着x的增大而增大，
∴S=S△APC+6
∴S在a＜x＜0上随着x的增大而增大，
当x≤a时，
∴AC=a-x，
∴PC=-
∴△APC的面积为S=（a-x）=-3（-1）
∵a＜0，
∴在x＜a随着x的增大而增大，
∴-1在x＜a上随着x的增大而增大，
∴-3（-1）在x＜a上随着x的增大而减小，
∴S=6-S△APC
∴S在x＜a上随着x的增大而增大，
∴当P的横坐标增大时，S的值是逐渐增大，
故选D．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
