题目内容
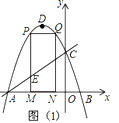
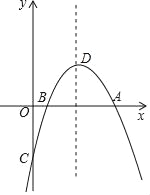
【题目】如图,抛物线y=ax2+bx+c与x轴交于A,B(1,0)两点,与y轴交于点C,直线y=![]() x﹣2经过A,C两点,抛物线的顶点为D.
x﹣2经过A,C两点,抛物线的顶点为D.
(1)求抛物线的解析式;
(2)求抛物线的顶点D的坐标;
(3)在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由;
(4)在直线AC的上方抛物线上是否存在点P,使△PAC的面积最大?若存在,直接写出P点坐标及△PAC面积的最大值.
【答案】(1)y=﹣![]() x2+
x2+![]() x﹣2;(2)顶点D(
x﹣2;(2)顶点D(![]() ,
,![]() );(3)存在点G(0,
);(3)存在点G(0,![]() )使得GD+GB的值最小.理由见解析;(4)在直线AC的上方抛物线上存在点P(2,1),使△PAC的面积最大,最大值为4.理由见解析.
)使得GD+GB的值最小.理由见解析;(4)在直线AC的上方抛物线上存在点P(2,1),使△PAC的面积最大,最大值为4.理由见解析.
【解析】
(1)利用一次函数是性质求得点A、C的坐标,然后把点A、B、C的坐标分别代入二次函数解析式,利用待定系数法求得二次函数解析式即可;
(2)将二次函数解析式转化为顶点式方程,可以直接得到答案;
(3)利用轴对称﹣最短路径方法证得点G,结合一次函数图象上点的坐标特征求得点G的坐标;
(4)利用分割法求得△PAC的面积为二次函数的形式,利用二次函数最值的求法进行解答.
(1)把x=0代入y=![]() x﹣2中得:y=﹣2,
x﹣2中得:y=﹣2,
把y=0代入y=![]() x﹣2中得:x=4,
x﹣2中得:x=4,
∴A(4,0),C(0,﹣2),
把A(4,0),B(1,0),C(0,﹣2)分别代入y=ax2+bx+c,得
 ,
,
解得 ,
,
则该抛物线的解析式为:y=﹣![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)由(1)知,该抛物线的解析式为y=﹣![]() x2+
x2+![]() x﹣2,
x﹣2,
∴y=﹣![]() x2+
x2+![]() x﹣2=﹣
x﹣2=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴顶点D(![]() ,
,![]() );
);
(3)存在点G(0,![]() )使得GD+GB的值最小.理由如下:
)使得GD+GB的值最小.理由如下:
如图1,作点B关于y轴的对称点B′,连接B′D交y轴于点G,则B′(﹣1,0).

设直线B′D的解析式为y=kx+b.
则 ,
,
解得: ,
,
∴直线B′D的解析式为y=![]() x+
x+![]() ,
,
把x=0代入,得y=![]() ,
,
∴存在点G(0,![]() )使得GD+GB的值最小;
)使得GD+GB的值最小;
(4)在直线AC的上方抛物线上存在点P(2,1),使△PAC的面积最大,最大值为4.理由如下:
如图2,过点P作PQ∥y轴交AC于Q,连接PC,PA.

设P(x,﹣![]() x2+
x2+![]() x﹣2),则Q(x,
x﹣2),则Q(x,![]() x﹣2).
x﹣2).
∴PQ=﹣![]() x2+
x2+![]() x﹣2﹣(
x﹣2﹣(![]() x﹣2)=﹣
x﹣2)=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣2)2+2.
(x﹣2)2+2.
又∵S△PAC=S△PQC+S△PQA=![]() xPQ+
xPQ+![]() (4﹣x)PQ=2PQ,
(4﹣x)PQ=2PQ,
∴S△PAC=﹣(x﹣2)2+4,
∴当x=2时,S△PAC最大值为4,此时﹣![]() x2+
x2+![]() x﹣2=1,
x﹣2=1,
∴在直线AC的上方抛物线上存在点P(2,1),使△PAC的面积最大,最大值为4.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案