题目内容
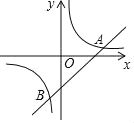
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为4.
(1)求抛物线的表达式;
(2)求∠CAB的正切值;
(3)如果点P是x轴上的一点,且∠ABP=∠CAO,直接写出点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)![]() ;(3)点P的坐标是(1,0)
;(3)点P的坐标是(1,0)
【解析】
(1) 先求得抛物线的对称轴方程, 然后再求得点C的坐标,设抛物线的解析式为y=a(x+1)2+4,将点 (-3, 0) 代入求得a的值即可;
(2) 先求得A、 B、 C的坐标, 然后依据两点间的距离公式可得到BC、AB,AC的长,然后依据勾股定理的逆定理可证明∠ABC=90°,最后,依据锐角三角函数的定义求解即可;
(3) 连接BC,可证得△AOB是等腰直角三角形,△ACB∽△BPO,可得![]() 代入个数据可得OP的值,可得P点坐标.
代入个数据可得OP的值,可得P点坐标.
解:(1)由题意得,抛物线y=ax2+2ax+c的对称轴是直线![]() ,
,
∵a<0,抛物线开口向下,又与x轴有交点,
∴抛物线的顶点C在x轴的上方,
由于抛物线顶点C到x轴的距离为4,因此顶点C的坐标是(﹣1,4).
可设此抛物线的表达式是y=a(x+1)2+4,
由于此抛物线与x轴的交点A的坐标是(﹣3,0),可得a=﹣1.
因此,抛物线的表达式是y=﹣x2﹣2x+3.
(2)如图1,
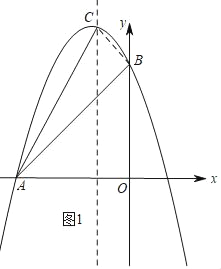
点B的坐标是(0,3).连接BC.
∵AB2=32+32=18,BC2=12+12=2,AC2=22+42=20,
得AB2+BC2=AC2.
∴△ABC为直角三角形,∠ABC=90°,
所以tan∠CAB=![]() .
.
即∠CAB的正切值等于![]() .
.
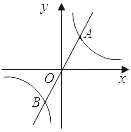
(3)如图2,连接BC,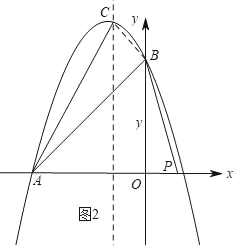
∵OA=OB=3,∠AOB=90°,
∴△AOB是等腰直角三角形,
∴∠BAP=∠ABO=45°,
∵∠CAO=∠ABP,
∴∠CAB=∠OBP,
∵∠ABC=∠BOP=90°,
∴△ACB∽△BPO,
∴![]() ,
,
∴![]() ,OP=1,
,OP=1,
∴点P的坐标是(1,0).

【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?