题目内容
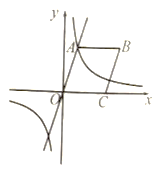
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
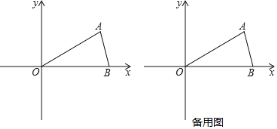
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
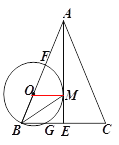
(3)设半径为2的⊙P与直线OA交于M、N两点,已知![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
【答案】(1)A点坐标为![]() ,B点坐标为(6,0);(2)
,B点坐标为(6,0);(2)![]() ;(3)m的值为
;(3)m的值为![]() 或
或![]()
【解析】
(1)根据30°角所对的直角边是斜边的一半,可得AC的长,再根据锐角三角函数,可得OC,根据点的坐标,可得答案;
(2)根据等腰直角三角形,可得E点坐标,再根据待定系数法,可得答案;
(3)根据30°角所对的直角边是斜边的一半,可得∠CNP=30°,再根据勾股定理求得OE的长,根据点的坐标,可得N点坐标,根据点的左右平移,可得点P坐标.
(1)如图1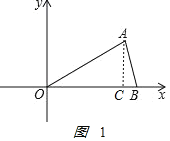 ,
,
作 AC⊥OB于C点,
由OB=OA=6,得B点坐标为(6,0),
由OB=OA=6,∠AOB=30°,得
![]() ,
,
∴A点坐标为![]() ;
;
(2)如图2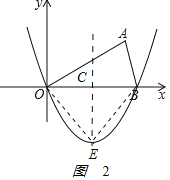 ,
,
由其顶点为E,当△OBE为等腰直角三角形,得
![]() ,
,
即E点坐标为(3,﹣3).
设抛物线的解析式为y=a(x﹣3)2﹣3,将B点坐标代入,解得![]() ,
,
抛物线的解析式为![]()
化简得![]() ;
;
(3)如图3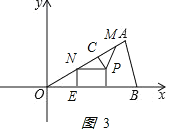 ,
,
PN=2, ![]() ,PC=1,
,PC=1,
∠CNP=∠AOB=30°,
NP∥OB,
NE=2,得ON=4,
由勾股定理,得
![]() ,即
,即![]() .
.
N向右平移2个单位得![]() ,
,
N向左平移2个单位,得![]() ,
,
m的值为![]() 或
或![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间(小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3
C. 平均数是3 D. 方差是0.34