题目内容
【题目】已知反比例函数![]() 与一次函数
与一次函数![]() (k≠0),一次函数的图象与y轴交于点C,与x轴交于点D.
(k≠0),一次函数的图象与y轴交于点C,与x轴交于点D.
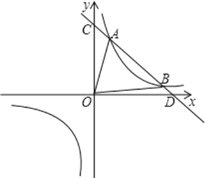
(1)当k=-1时,如图,设直线![]() 与双曲线
与双曲线![]() 的两个交点为A、B(B在A的右边),求△OAB的面积;
的两个交点为A、B(B在A的右边),求△OAB的面积;
(2)若直线![]() 与双曲线
与双曲线![]() 总有两个不同的交点,求k的取值范围;
总有两个不同的交点,求k的取值范围;
(3)若直线![]() 与双曲线
与双曲线![]() 交于不同的两点M(
交于不同的两点M(![]() )、N(
)、N(![]() ),且满足
),且满足![]() ,求k的值.
,求k的值.
【答案】(1)![]() ;(2)
;(2)![]() 且k≠0;(3)k=1或
且k≠0;(3)k=1或![]()
【解析】
(1)首先联立两个函数的解析式求得交点坐标,再用![]() 得到面积.
得到面积.
(2)首先联立两个函数的解析式得到一个一元二次方程,把交点问题转化为一元一次方程又多少解的问题,根据根的判别式去判断.
(3)首先联立两个函数的解析式得到一个一元二次方程,根据韦达定理得到两根之积与两根之和的值,再把![]() 两边平方,代入求解即可.
两边平方,代入求解即可.
(1)联立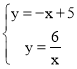 ,得
,得![]() 或
或![]() , ∴A(2,3),B(3,2)
, ∴A(2,3),B(3,2)
又D(5,0)∴![]()
(2)由 ![]() =
=![]() ,得
,得![]() ,△=25+24k>0,∴
,△=25+24k>0,∴![]() 且k≠0;
且k≠0;
(3)由 ![]() =
=![]() ,得
,得![]() ,∴
,∴![]() 、
、![]() 为方程
为方程![]() 的两个不相等的实数根.
的两个不相等的实数根.
则![]() +
+![]() =
=![]() ,
,![]()
则![]()
=![]()
解得k=1或![]() 且均为方程的解
且均为方程的解
∴k=1或![]() .
.

练习册系列答案
相关题目
【题目】小明将小球沿地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度![]() (
(![]() )与它的飞行时间
)与它的飞行时间![]() (
(![]() )满足二次函数关系,
)满足二次函数关系,![]() 与
与![]() 的几组对应值如下表所示:
的几组对应值如下表所示:

|
|
|
|
|
| … |
|
|
|
|
|
| … |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写
的函数解析式(不要求写![]() 的取值范围)
的取值范围)
(2)问:小球的飞行高度能否达到![]() ?请说明理由
?请说明理由