题目内容
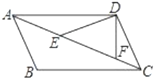
【题目】如图,![]() 、
、![]() 是等腰
是等腰![]() 两腰上的高,
两腰上的高,![]() 、
、![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)点![]() 在边
在边![]() 的延长线上,过
的延长线上,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
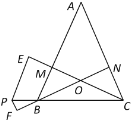
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)根据“AAS”证明△BMC≌△CNB,可得∠OBC=∠OCB,再根据经等角对等边可证结论成立;
(2)由![]() =
=![]() -
-![]() ,可得PE-PF=BM,由△BOM∽△BAN,得
,可得PE-PF=BM,由△BOM∽△BAN,得![]() ,再证明AM=AN,代入整理可证结论成立.
,再证明AM=AN,代入整理可证结论成立.
解:(1)∵等腰△ABC中,AB=AC,
∴∠ABC=∠ACB,
∵CM⊥AB,BN⊥AC,
∴∠BMC=∠CNB=90°,
又∵BC=BC,
∴△BMC≌△CNB,
∴∠OBC=∠OCB,
∴OB=OC;
(2)连接OP,
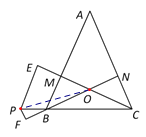
∵PE//AB,PF//AC,
∴∠PEC=∠BMC=90°,∠PFB=∠CNB=90°.
∵![]() =
=![]() -
-![]() ,
,
∴![]() OC·BM=
OC·BM=![]() OC·PE-
OC·PE-![]() OB·PF,
OB·PF,
∵OB=OC,
∴PE-PF=BM.
∵∠BMC=∠ANB=90°,∠BMO=∠NBA,
∴△BOM∽△BAN,
∴![]() ,
,
∴OM·BN=BM·AN=(PE-PF)·AN.
∵△BMC≌△CNB,
∴BM=CN,
∵AB=AC,
∴AM=AN,
∴OM·BN=(PE-PF)·AM,
∴AM·PF+OM·BN=AM·PE.

练习册系列答案
相关题目