题目内容
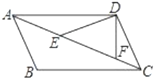
【题目】如图，
、
在
的对角线
上，
，
，
，则
的大小为（ ）．
A.
B.
C.
D.
【答案】D
【解析】
设∠ADE=x，由直角三角形的性质得出DE=
AF=AE=EF，从而∠DAE=∠ADE=x， DE=CD，证出∠DCE=∠DEC=2x，由AD//BC得∠ACB=∠DAE=x，然后根据∠BCD =54°，得出方程，解方程即可．
解：设∠ADE=x，
∵AE=EF，∠ADF=90°，
∴DE=AF=AE=EF，
∴∠DAE=∠ADE=x，
∵AE=EF=CD，
∴DE=CD，
∴∠DCE=∠DEC=2x，
∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠ACB=∠DAE =x，
∵∠BCD =54°，
∴2x+x=54°，
解得：x=18°，
即∠ADE=18°．
故选D．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长，随机抽取了
名九年级学生做网络问卷调查．共四个选项：
小时以下)、
小时)、
小时)， 
小时以上)，每人只能选一
项．并将调查结果绘制成如下不完整的统计表和统计图．
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
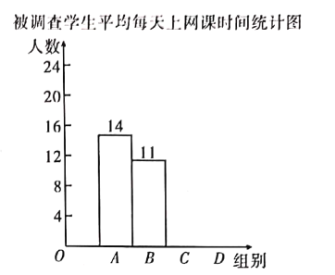
根据以上信息，解答下列问题：
，
，
补全条形统计图；
该校有九年级学生
名，请你估计仝校九年级学生平均每天上网课时长在
小时及以上的共多少名；
在被调查的对象中，平均每天观看时长超过
小时的，有
名来自九
班，
名来自九
班，其余都来自九班，现教导处准备从
选项中任选两名学生进行电话访谈，请用列表法或画树状图的方法求所抽取的名学生恰好来自同一个班级的概率．
