题目内容
【题目】直线![]() 与双线
与双线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为第三象限内一点.
为第三象限内一点.
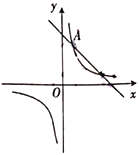
(1)如图1,若点![]() 的坐标为
的坐标为![]() .
.
①![]() ______,点
______,点![]() 的坐标为______.
的坐标为______.
②不等式![]() 的解集为______.
的解集为______.
③当![]() ,且
,且![]() 时,求点
时,求点![]() 的坐标.
的坐标.
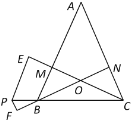
(2)如图2,当![]() 为等边三角形时,点
为等边三角形时,点![]() 的坐标为
的坐标为![]() ,试求
,试求![]() 、
、![]() 之间的关系式.
之间的关系式.
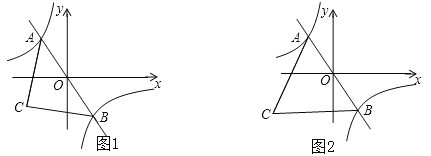
【答案】(1)①-2,![]() ;②
;②![]() 或
或![]() ;③
;③![]() ;(2)mn=18
;(2)mn=18
【解析】
(1)①直接把点A的坐标代入反比例函数解析式,即可求出a;
由双曲线的对称性可知点A和点B关于原点对称,由关于原点对称的点横纵坐标分别互为相反数可得点B的坐标;
②结合图象可得求![]() 即为求使得直线在双曲线上方时自变量x的取值范围;
即为求使得直线在双曲线上方时自变量x的取值范围;
③连接CO,作AD⊥y轴于D点,作CE垂直y轴于E点,根据直角三角形斜边的中线等于斜边的一半和互余关系,可证得△ADO≌△OEC,由A点的坐标可得CE=OD=3,EO=DA=2,从而确定点C的坐标;
(2)连接CO,作AD⊥y轴于D点,作CE垂直y轴于E点,根据等边三角形的性质,可得∠ACO=30°,可证明△ADO∽△OEC,由相似三角形的性质和锐角三角函数可用m、n表示出A点的坐标,代入反比例函数解析式可得到m、n间关系.
解:(1)①∵A(a,3)在双曲线![]() 上,
上,
∴![]() ,
,
∴a=-2;
∵点A和点B在直线![]() 上和双曲线上,
上和双曲线上,
∴点A和点B关于原点对称,
∵A(-2,3),
∴B(2,-3).
故答案为:-2,![]() ;
;
②由图象可知直线在双曲线上方时对应的自变量x的取值范围为:![]() 或
或![]() ,
,
故![]() 的解集为
的解集为![]() 或
或![]() ;
;
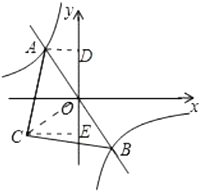
③如图,连接![]() ,作
,作![]() 轴于
轴于![]() ,
,![]() 轴
轴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中
中
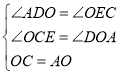
![]() (AAS).
(AAS).
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)连接CO,作AD⊥y轴于D点,作CE⊥y轴于E点,
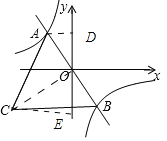
∵反比例函数和正比例函数都是中心对称图形,它们都关于原点对称,
∴OA=OB,
又∵△ABC为等边三角形,
∴∠AOC=∠BOC=90°,
∵∠AOD+∠DAO=90°,∠COE+∠BOE=90°,∠DOA=∠BOE,
∴∠DAO=∠COE,
∴△ADO∽△OEC,
∴![]() ,
,
由于∠ACO=30°,
![]() ,
,
因为C的坐标为(m, n),
所以CE=-m,OE=-n,
∴AD=![]() ,OD=
,OD=![]() ,
,
所以A(![]() ,
,![]() ).
).
代入![]() 中,
中,
得mn=18.

【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
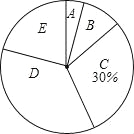
【题目】今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
(1)求全班学生人数和m的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
分组 | 分数段(分) | 频数 |
A | 36≤x<41 | 2 |
B | 41≤x<46 | 5 |
C | 46≤x<51 | 15 |
D | 51≤x<56 | m |
E | 56≤x<61 | 10 |