题目内容
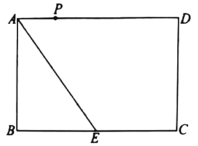
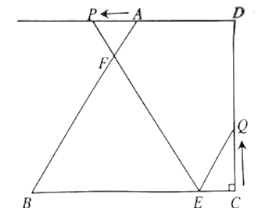
【题目】如图，矩形ABCD中，AB=2，AD=4，M点是BC的中点，A为圆心，AB为半径的圆交AD于点E．点P在弧BE上运动，则PM+
DP的最小值为____________．
【答案】
【解析】
取AE的中点K，连接PK，KM，作KH⊥BC于H，则四边形ABHK是矩形．可得AK=BH=1，HK=AB=2．由△PAK∽△DAP，推出
，推出
，推出
，由
，求出KM即可解决问题．
解：
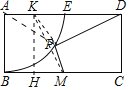
取AE的中点K，连接PK，KM，作KH⊥BC于H，则四边形ABHK是矩形．可得AK=BH=1，HK=AB=2，
∵AP=2，AK=1，AD=4，
∴PA2=AKAD，
∴
∵∠KAP=∠PAD，
∴△PAK∽△DAP，
∴，
∴，
∴，
∵，
，
∴
，
∴
的最小值为，
故答案为：.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长，随机抽取了
名九年级学生做网络问卷调查．共四个选项：
小时以下)、
小时)、
小时)， 
小时以上)，每人只能选一
项．并将调查结果绘制成如下不完整的统计表和统计图．
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
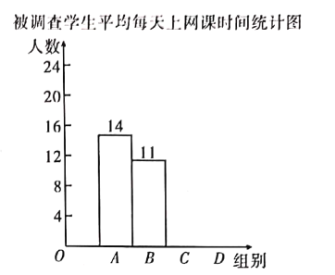
根据以上信息，解答下列问题：
，
，
补全条形统计图；
该校有九年级学生
名，请你估计仝校九年级学生平均每天上网课时长在
小时及以上的共多少名；
在被调查的对象中，平均每天观看时长超过
小时的，有
名来自九
班，
名来自九
班，其余都来自九班，现教导处准备从
选项中任选两名学生进行电话访谈，请用列表法或画树状图的方法求所抽取的名学生恰好来自同一个班级的概率．
