题目内容
【题目】如图①,在△ABC中,AB=AC,∠BAC=![]() (
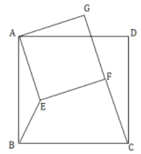
(![]() <45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.
<45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.
(1)四边形ABDF的形状是 ;
(2)求证:四边形AEDG是平行四边形;
(3)若AB=2,![]() =30°,则四边形AEDG的面积是 .
=30°,则四边形AEDG的面积是 .

【答案】(1)正方形;(2)见解析;(3)![]()
【解析】
(1)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形,再由旋转角是90°,即可得出结论;
(2)由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论.
(3)过B作BH⊥AC于H,过点E作EM⊥AB于M,作∠BEN=∠ABE交AB于N,利用直角三角形的性质分别求出BH,AH,CH,BE,BC,计算出∠MNE=30°,设ME=x,则NE=2x,BN=x,利用勾股定理Rt△BME中解出x值,即ME的长度,再利用S四边形AEDG=S正方形ABDF-2S△DBE-2S△ABE计算结果即可.
解:(1)四边形ABDF是正方形,
证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的,
∴∠DBA=∠FAB=90°,DB=AB=AF,AC=DE=AG,
∴∠DBA+∠FAB=180°,
∴DB∥AF,
∵AB=AC,
∴AB=DB=FA=AC=DE=AG,
∵DB∥AF,DB=AF
∴四边形ABDF是平行四边形,
∵∠ABD=90°,
∴四边形ABDF是矩形,
∵AB=DB,
∴平行四边形ABDF是正方形;
(2)∵四边形ABDF是正方形,
∴∠DFA=∠DBA=90°,AB=DF,
∴∠ABD-∠DBE=∠AFD-∠AFG,
∴∠EBA=∠GFD,
在△ABE和△DFG中,
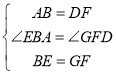 ,
,
∴△ABE≌△DFG(SAS),
∴AE=DG,
又∵DE=AG=AB,
∴四边形AEDG是平行四边形.
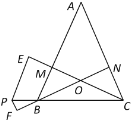
(3)过B作BH⊥AC于H,过点E作EM⊥AB于M,作∠BEN=∠ABE交AB于N,
∵AB=2,∠BAC=30°,
∴BH=![]() AB=1,
AB=1,
AH=![]() ,
,
∴CH=AC-AH=AB-AH=2-![]() ,
,
∴BC=![]() =
=![]() ,
,
∴BE=BC=![]() ,
,
∵∠BDE=∠BAC=α=30°,DB=DE,
∴∠DBE=∠DEB=![]() =75°,
=75°,
∴∠ABE=∠ABD-∠DBE=90°-75°=15°,
∴∠BEN=∠ABE=15°,
∴∠MNE=∠NBE+∠BEN=15°+15°=30°,
设ME=x,则NE=2x,BN=x,
MN=![]() ,
,
∴BM=BN+NM=2x+![]() x,
x,
在Rt△BME中,BM2+ME2=BE2,
即![]() ,
,
解得![]() ,
,![]() (舍),
(舍),
∴x=![]() ,
,
∴ME=![]() ,
,
∴S△DBE=S△ABC=![]() AC×BH=
AC×BH=![]() ×2×1=1,
×2×1=1,
S△ABE=![]() AB×ME=
AB×ME=![]() ×2×(
×2×(![]() )=
)=![]() ,
,
∴S四边形AEDG
=S正方形ABDF-2S△DBE-2S△ABE
=![]()
=![]()


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案