ЬтФПФкШн
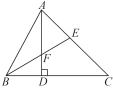
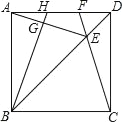
ЁОЬтФПЁПЃЈ1ЃЉРЯЪІдкПЮЩЯИјГіСЫетбљвЛЕРЬтФПЃКШчЭМЃЈ1ЃЉЃЌЕШБпЁїABCБпГЄЮЊ2ЃЌЙ§ABБпЩЯвЛЕуPзїPEЁЭACгкEЃЌQЮЊBCбгГЄЯпЩЯвЛЕуЃЌЧвAP=CQЃЌСЌНгPQНЛACгкDЃЌЧѓDEЕФГЄ.
аЁУїЭЌбЇОЙ§ШЯецЫМПМКѓШЯЮЊЃЌПЩвдЭЈЙ§Й§ЕуPзїЦНааЯпЙЙдьЕШБпШ§НЧаЮЕФЗНЗЈРДНтОіетИіЮЪЬт.ЧыИљОнаЁУїЭЌбЇЕФЫМТЗжБНгаДГіDEЕФГЄ.
ЃЈ2ЃЉЃЈРрБШЬНОПЃЉ
РЯЪІв§ЕМЭЌбЇМЬајбаОПЃК
ЂйЕШБпЁїABCБпГЄЮЊ2ЃЌЕБPЮЊBAЕФбгГЄЯпЩЯвЛЕуЪБ,зїPEЁЭCAЕФбгГЄЯпгкЕуE ЃЌQЮЊБпBCЩЯвЛЕуЃЌЧвAP=CQЃЌСЌНгPQНЛACгкD.ЧыФудкЭМЃЈ2ЃЉжаВЙШЋЭМаЮВЂЧѓDEЕФГЄ.
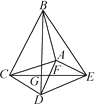
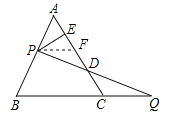
ЂквбжЊЕШБпЁїABCЃЌЕБPЮЊABЕФбгГЄЯпЩЯвЛЕуЪБ,зїPEЁЭЩфЯпACгкЕуEЃЌ QЮЊФФвЛИіЃЈЂйBCБпЩЯЃЛЂкBCЕФбгГЄЯпЩЯЃЛЂлCBЕФбгГЄЯпЩЯЃЉвЛЕуЃЌЧвAP=CQЃЌСЌНгPQНЛжБЯпACгкЕуDЃЌФмЪЙЕУDEЕФГЄЖШБЃГжВЛБф.( жБНгаДГіД№АИЕФБрКХ)
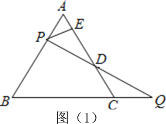
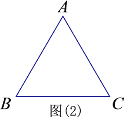
ЁОД№АИЁПЃЈ1ЃЉDE=1ЃЛ(2) Ђйе§ШЗВЙШЋЭМаЮМћНтЮіЃЌЂк Ђк.
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§PзїPFЁЮBCНЛACгкFЃЌЕУГіЕШБпШ§НЧаЮAPFЃЌЭЦГіAP=PF=QCЃЌИљОнЕШбќШ§НЧаЮаджЪЧѓГіEF=AEЃЌжЄЁїPFDЁеЁїQCDЃЌЭЦГіFD=CDЃЌЭЦГіDE![]() ACМДПЩЃЛ
ACМДПЩЃЛ
ЃЈ2ЃЉЂйЙ§ЕуPзїPFЁЮBCНЛCAЕФбгГЄЯпгыЕуFЃЌгЩЦНааЯпЕФаджЪЕУГіЁЯPFA=ЁЯCЃЎ
дйжЄУїЁїAPFЮЊЕШБпШ§НЧаЮЃЌЕУЕНAP=PFЃЎНјвЛВНЕУЕНAE=FE=![]() ЃЎгЩSASжЄУїЁїFDPЁеЁїCDQЃЌЕУЕНFD=CD=
ЃЎгЩSASжЄУїЁїFDPЁеЁїCDQЃЌЕУЕНFD=CD=![]() ЃЌИљОнЯпЖЮЕФКЭВюМДПЩЕУЕННсТлЃЎ
ЃЌИљОнЯпЖЮЕФКЭВюМДПЩЕУЕННсТлЃЎ
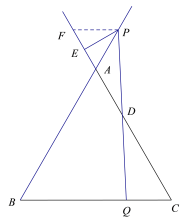
ЂкШчЭМЃЌЙ§PзїжБЯпPFЁЮBCНЛжБЯпACгкFЃЌЭЈЙ§жЄУїЁїAPFЪЧЕШБпШ§НЧаЮЃЌЕУЕНAP=PFЃЎНјЖјЕУЕНEF=AE=![]() AFЃЎдйгЩЯпЖЮЕФКЭВюМДПЩЕУГіНсТлЃЎ
AFЃЎдйгЩЯпЖЮЕФКЭВюМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЙ§PзїPFЁЮBCНЛACгкFЃЎ
ЁпPFЁЮBCЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрЁЯPFD=ЁЯQCDЃЌЁїAPFЪЧЕШБпШ§НЧаЮЃЌЁрAP=PF=AFЃЎ
ЁпPEЁЭACЃЌЁрAE=EFЃЎ
ЁпAP=PFЃЌAP=CQЃЌЁрPF=CQЃЎ
дкЁїPFDКЭЁїQCDжаЃЌЁп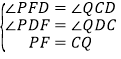 ЃЌЁрЁїPFDЁеЁїQCDЃЈAASЃЉЃЌЁрFD=CDЃЎ
ЃЌЁрЁїPFDЁеЁїQCDЃЈAASЃЉЃЌЁрFD=CDЃЎ
ЁпAE=EFЃЌЁрEF+FD=AE+CDЃЌЁрAE+CD=DE![]() ACЃЎ
ACЃЎ
ЁпAC=2ЃЌЁрDE=1ЃЎ
(2)Ђйе§ШЗВЙШЋЭМаЮЃЎ
Й§ЕуPзїPFЁЮBCНЛCAЕФбгГЄЯпгыЕуFЃЌЁрЁЯPFA=ЁЯCЃЎ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрЁЯBAC=ЁЯC=60ЁуЃЌЁрЁЯPFA=ЁЯPAF=60ЁуЃЌЁрЁїAPFЮЊЕШБпШ§НЧаЮЃЌЁрAP=PFЃЎ
гжЁпPEЁЭCAЕФбгГЄЯпгкЕуEЃЌЁрAE=FE=![]() ЃЎ
ЃЎ
ЁпAP=CQЃЌЁрPF=QCЃЎ
ЁпЁЯFDP=ЁЯCDQЃЌЁрЁїFDPЁеЁїCDQЃЌЁрFD=CD=![]() ЃЌЁрDE=DFЉEF=
ЃЌЁрDE=DFЉEF=![]() ЃЎ
ЃЎ
Ђк Д№АИЮЊЂкЃЎРэгЩШчЯТЃК
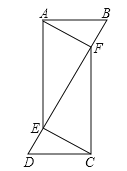
ШчЭМЃЌЙ§PзїжБЯпPFЁЮBCНЛжБЯпACгкFЃЌЁрЁЯAPF=ЁЯABC=60ЁуЃЎ
ЁпЁЯA=60ЁуЃЌЁрЁїAPFЪЧЕШБпШ§НЧаЮЃЌЁрAP=PFЃЎ
ЁпAP=CQЃЌЁрPF=QCЃЎ
ЁпPFЁЮBCЃЌЁрЁЯF=ЁЯDCQЃЌЁЯFPD=ЁЯQЃЎ
дкЁїDPFКЭЁїDQCжаЃЌЁпЁЯF=ЁЯDCQЃЌPF=QCЃЌЁЯFPD=ЁЯQЃЌЁрЁїDPFЁеЁїDQCЃЌЁрCD=DF=![]() CFЃЎ
CFЃЎ
ЁпЁїAPFЪЧЕШБпШ§НЧаЮЃЌPEЁЭAFЃЌЁрEF=AE=![]() AFЃЎ
AFЃЎ
ЁпED=EFЉDFЃЌЁрED=![]() AFЉ
AFЉ![]() CF=
CF=![]() ЃЈAFЉCFЃЉ=
ЃЈAFЉCFЃЉ=![]() ACЃЎ
ACЃЎ
ЁпACЕФГЄЖШВЛБфЃЌЁрDEЕФГЄЖШБЃГжВЛБфЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ