题目内容
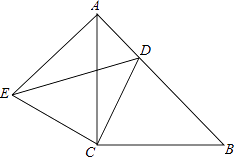
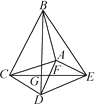
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S四边形BCDE=![]() BD·CE;⑤BC2+DE2=BE2+CD2.其中正确的结论有( )
BD·CE;⑤BC2+DE2=BE2+CD2.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据等腰直角三角形的性质可得AB=AC,AD=AE,然后求出∠BAD=∠CAE,再利用“边角边"证明△ABD和△ACE全等,根据全等三角形对应边相
等可得CE=BD,判断①正确;根据全等三角形对
应角相等可得∠ABD=∠ACE,从而求出∠BCG+∠CBG=∠ACB+∠ABC=90°,再求出∠BGC=90°,从而得到BD⊥CE,根据四边形的面积判断出
④正确;根据勾股定理表示出![]() ,得到⑤正确;再求出AE∥CD时,∠ADC=90°,判断出②错误;∠AEC与∠BAE不一定相等判断出③错误.
,得到⑤正确;再求出AE∥CD时,∠ADC=90°,判断出②错误;∠AEC与∠BAE不一定相等判断出③错误.
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC, AD=AE,
∴∠BAD=∠BAC+∠CAD=90°+∠CAD,
∠CAE=∠DAE+∠CAD=90+∠CAD
∴∠BAD=∠CAE
在△ABD和△ACE中,
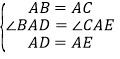
∴△ABD≌△ACE(SAB),
∴CE=BD,①正确;
∠ABD=∠ACF
∠BCG+∠CBG=∠ACB+∠ABC=90°,
在△BCG中,∠BGC=180°-(∠BCG+∠CBG)
=180°- 90°=90°
∴BD⊥CE,
∴四边形ABCD的面积=![]() 故④正确;
故④正确;
由勾股定理,在Rt△BCG中![]()
由勾股定理,在Rt△DEG中,![]()
∴![]()
在Rt△BGE中,![]()
在Rt△CDG中,![]()
∴![]()
∴![]()
故⑤正确;
只有AE∥CD时,∠AEC=∠DCE,
∠ADC=∠ADB+∠BDC=90°
无法说明AE∥CD,故②错误;
∵△ABD≌△ACE
∴∠ADB=∠AEC
∵∠AEC与∠AEB相等无法证明,
∴∠ADB=∠AEB不一定成立,故③错误;
综上所述,正的结论有①④⑤共3个.
故选C.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案