题目内容
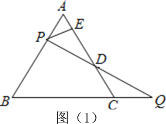
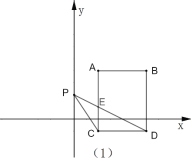
【题目】如图,在正方形ABCD对角线BD上截取BE=BC,连接CE并延长交AD于点F,连接AE,过B作BG⊥AE于点G,交AD于点H,则下列结论错误的是( )
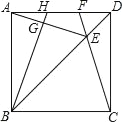
A. AH=DF B. S四边形EFHG=S△DCF+S△AGH
C. ∠AEF=45° D. △ABH≌△DCF
【答案】B
【解析】分析:先判断出∠DAE=∠ABH,再判断△ADE≌△CDE得出∠DAE=∠DCE=22.5°,∠ABH=∠DCF,再判断出Rt△ABH≌Rt△DCF从而得到A、D正确,根据三角形的外角求出∠AEF=45°,得出C正确;连接HE,判断出S△EFH≠S△EFD得出B错误.
详解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,
在Rt△ABH中,∠AHB=90°-∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中
 ,
,
∴△ADE≌△CDE,
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在Rt△ABH和Rt△DCF中
 ,
,
∴Rt△ABH≌Rt△DCF,
∴AH=DF,∠CFD=∠AHB=67.5°,
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故ACD正确;
如图,连接HE,

∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故B错误,
故选:B.

【题目】某班将举行知识竞赛活动,班长安排小明购买奖品.小明去文化用品店买了两种大小不同的笔记本一共a本,其中大笔记本单价8元,小笔记本单价5元.若设买单价5元小笔记本买了x本.
(1)填写下表:
单价(元/本) | 数量(本) | 金额(元) | |
小笔记本 | 5 | x | 5x |
大笔记本 | 8 |
(2)列式表示:小明买大小笔记本共花 元.
(3)若小明从班长那里拿了300元,买了40本大小不同的两种笔记本(a=40),还找回55元给班长,那么小明买了大小笔记本各多少本?
(4)若这个班下次活动中,让小明刚好花400元购买这两种大小笔记本,并且购买的小笔记本数量x要小于60本,但还要超过30本(30<x<60),请列举小明有可能购买的方案,并说明理由.
【题目】某网站策划了A、B两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 30 | 25 | 0.05 |
B | m | n | P |
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)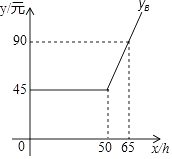
(1)m=;n=p= .
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?