题目内容
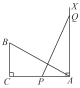
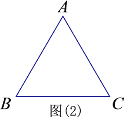
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的平分线BE交AD于点F,则图中共有等腰三角形( )
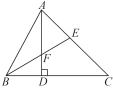
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】
根据在△ABC中,∠ABC=60°,∠ACB=45°,利用三角形内角和定理求得∠BAC=75°,然后可得等腰三角形.
∵∠ABC=60°,∠ACB=45°,AD是高,
∴∠DAC=45°,
∴CD=AD,
∴△ADC为等腰直角三角形,
∵∠ABC=60°,BE是∠ABC平分线,
∴∠ABE=∠CBE=30°,
在△ABD中,∠BAD=180°∠ABD∠ADB=180°60°90°=30°,
∴∠ABF=∠BAD=30°,
∴AF=BF即△ABF是等腰三角形,
在△ABC中,∠BAC=180°∠ABC∠ACB=180°60°45°=75°,
∵∠AEB=∠CBE+∠ACB=30°+45°=75°,
∴∠BAE=∠BEA,
∴AB=EB即△ABE是等腰三角形,
∴等腰三角形有△ACD,△ABF,△ABE;
故答案选:B.

练习册系列答案
相关题目