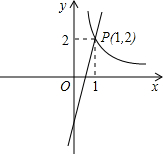题目内容
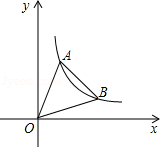
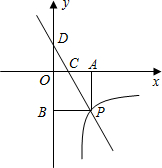
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、点D,与反比例函数y=
的图象在第四象限的相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6),且S△DBP=27
(1)求上述一次函数与反比例函数的表达式;
(2)求一次函数与反比例函数的另一个交点坐标.
| m |
| x |
(1)求上述一次函数与反比例函数的表达式;
(2)求一次函数与反比例函数的另一个交点坐标.

(1)令一次函数解析式y=kx+3中x=0,解得y=3,
∴D坐标为(0,3),即OD=3,
又B(0,-6),即OB=6,
∴BD=OD+OB=3+6=9,
∵SRt△BDP=
BD•BP=
×9×BP=27,
∴BP=6,
∴P的坐标为(6,-6),
将x=6,y=-6代入一次函数解析式得:-6=6k+3,
解得:k=-
,
∴一次函数解析式为y=-
x+3,
将x=6,y=-6代入反比例解析式得:-6=
,
解得:m=-36,
∴反比例函数的表达式为y=-
;
(2)联立两个关系式得:
,
消去y得:-
x+3=-
,
整理得:(x-6)(x+4)=0,
解得:x1=6,x2=-4,
经检验是原方程的解,
∴y1=-6,y2=9,
∴一次函数与反比例函数交点为(6,-6)或(-4,9),
则一次函数与反比例函数的另一交点坐标为(-4,9).
∴D坐标为(0,3),即OD=3,
又B(0,-6),即OB=6,
∴BD=OD+OB=3+6=9,
∵SRt△BDP=
| 1 |
| 2 |
| 1 |
| 2 |
∴BP=6,
∴P的坐标为(6,-6),
将x=6,y=-6代入一次函数解析式得:-6=6k+3,
解得:k=-
| 3 |
| 2 |
∴一次函数解析式为y=-
| 3 |
| 2 |
将x=6,y=-6代入反比例解析式得:-6=
| m |
| 6 |
解得:m=-36,
∴反比例函数的表达式为y=-
| 36 |
| x |
(2)联立两个关系式得:
|
消去y得:-
| 3 |
| 2 |
| 36 |
| x |
整理得:(x-6)(x+4)=0,
解得:x1=6,x2=-4,
经检验是原方程的解,
∴y1=-6,y2=9,
∴一次函数与反比例函数交点为(6,-6)或(-4,9),
则一次函数与反比例函数的另一交点坐标为(-4,9).

练习册系列答案
相关题目

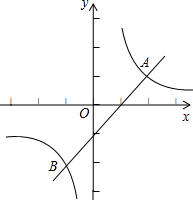
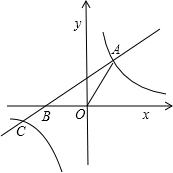
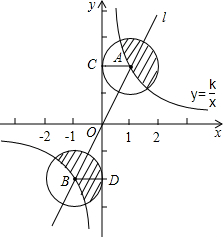 点A(1,2),点B(m,-2).分别过A、B作AC⊥y轴于C,BD⊥y轴于D,再以AC、BD为半径作⊙A和⊙B.
点A(1,2),点B(m,-2).分别过A、B作AC⊥y轴于C,BD⊥y轴于D,再以AC、BD为半径作⊙A和⊙B.