题目内容
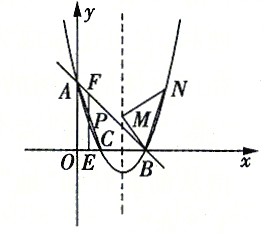
【题目】如图,在边长为6的菱形ABCD中,对角线AC,BD交点与点O,点P是△ADO的重心.
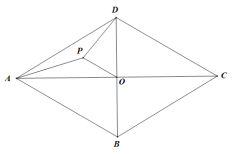
(1)当菱形ABCD是正方形时,则PA=________,PD=__________,PO=_________.
(2)线段PA,PD,PO中是否存在长度保持不变的线段,若存在,请求出该线段的长度,若不存在,请说明理由.
(3)求线段PD,DO满足的等量关系,并说明理由.
【答案】(1)![]() ;
;![]() ;2 (2)存在;PO=2 (3)见解析
;2 (2)存在;PO=2 (3)见解析
【解析】
(1)由正方形的性质和勾股定理可求出AE的长,由P点是△ADO的重心,根据重心的性质即可求出PA,PD的长,由直角三角形斜边上的中线等于斜边的一半,即可求出OP的长;
(2)延长OP交AD于G,由OG是Rt△AOD的斜中线可知OG=3,再利用重心的性质可得OP为定值;
(3)延长DP交AC于F,由菱形的对角线互相垂直及勾股定理可得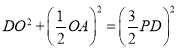 ,在△AOD中,由勾股定理得
,在△AOD中,由勾股定理得![]() ,即可得出线段PD,DO满足的等量关系.
,即可得出线段PD,DO满足的等量关系.
(1)PA=![]() ,PD=
,PD=![]() ,PD=2
,PD=2
当菱形ABCD是正方形时,如图,

∵正方形边长为6,点P是△ADO的重心,
∴![]() ,
,![]() ,
,
由勾股定理得,
![]() ,
,
∴![]() ,
,
∴PD=![]() ,
,
∵OG是△ADO的中线,
∴OG=![]() ,
,
∴![]() ;
;
(2)延长OP交AD于G
∵OG是Rt△AOD的斜中线
∴OG=![]()
∵P为重心
∴PO=![]()
∴PO为定值.
(3)延长DP交AC于F


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目