题目内容
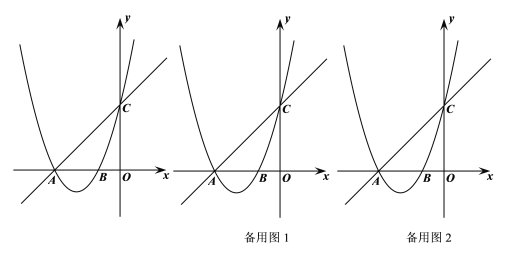
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 直线
直线![]() 经过点
经过点![]() .
.
(1)求抛物线的解析式;
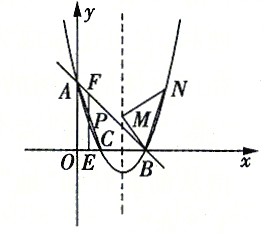
(2)点![]() 是直线
是直线![]() 下方的抛物线上一动点,过点
下方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限对称轴右侧抛物线上的一点,连接
是第一象限对称轴右侧抛物线上的一点,连接![]() 抛物线的对称轴上是否存在点
抛物线的对称轴上是否存在点![]() .使得
.使得![]() 与
与![]() 相似,且
相似,且![]() 为直角,若存在,请直接写出点
为直角,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2) ![]() 或
或![]() ;(3)存在,点
;(3)存在,点![]() 坐标为
坐标为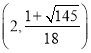 或
或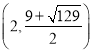
【解析】
(1)先求出点A、B坐标,用待定系数法即求出抛物线解析式;
(2)根据抛物线解析式与直线解析式表示出点P、F的坐标,然后表示出PE、PF,再列出绝对值方程,然后求解即可;
(3)先求出点C的坐标,也就求出OC的长,再设对称轴与![]() 轴交于点
轴交于点![]() 过
过![]() 点作
点作![]() 交对称轴于点
交对称轴于点![]() .根据相似三角形的性质得到KM和MQ的长,进而表示出点N的坐标,最后将点N的坐标代入函数解析式求解即可.
.根据相似三角形的性质得到KM和MQ的长,进而表示出点N的坐标,最后将点N的坐标代入函数解析式求解即可.
![]() 经过点
经过点![]() 分别在
分别在![]() 轴与
轴与![]() 轴上,
轴上,
![]() .
.
![]() 抛物线
抛物线![]() 经过点
经过点![]() ,
,
![]() ,解得
,解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]()
![]() 由题意可知,点
由题意可知,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 当点
当点![]() 在
在![]() 轴上方时,
轴上方时,
![]()
解得![]() 或
或![]() (与点
(与点![]() 重合,舍去).
重合,舍去).
![]()
![]() 当点
当点![]() 在
在![]() 轴下方时,
轴下方时,
![]()
解得![]() 或
或![]() (与点
(与点![]() 重合,舍去).
重合,舍去).
![]()
综上所述,![]() 的值为
的值为![]() 或
或![]()
![]() 存在,点
存在,点![]() 坐标为
坐标为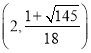 或
或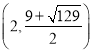
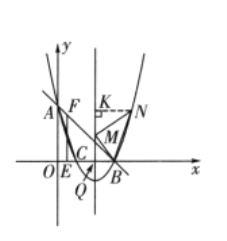
如图,设对称轴与![]() 轴交于点
轴交于点![]() 过
过![]() 点作
点作![]() 交对称轴于点
交对称轴于点![]() .
.
![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,
![]()
![]()
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]()
![]() 当
当![]() 时,
时,![]()
由一线三垂直模型得出,
![]() .
.
![]()
![]() 设
设![]()
则![]()
![]()
![]()
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]()
解得![]() (舍).
(舍).
![]() 点
点![]() 的坐标为
的坐标为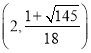
![]() 当
当![]() 时,
时,![]()
同理![]()
![]()
![]() ,
,
设![]()
则![]()
![]()
![]() 即
即![]()
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]()
解得![]() (舍),
(舍),
![]() 点
点![]() 的坐标为
的坐标为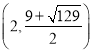
综上所述,存在点![]() 点
点![]() 的坐标为
的坐标为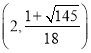 ,
,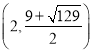

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.