题目内容
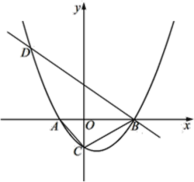
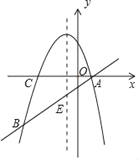
【题目】如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解板式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
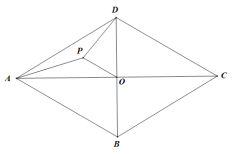
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)点P(![]() ,
,![]() );(3)符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).
);(3)符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).
【解析】
(1)令y=0,求出点A的坐标,根据抛物线的对称轴是x=﹣1,求出点C的坐标,再根据待定系数法求出抛物线的解析式即可;
(2)设点P(m,﹣m2﹣2m+3),利用抛物线与直线相交,求出点B的坐标,过点P作PF∥y轴交直线AB于点F,利用S△ABP=S△PBF+S△PFA,用含m的式子表示出△ABP的面积,利用二次函数的最大值,即可求得点P的坐标;
(3)求出点E的坐标,然后求出直线BC、直线BE、直线CE的解析式,再根据以点B、E、C、D为顶点的四边形是平行四边形,得到直线D1D2、直线D1D3、直线D2D3的解析式,即可求出交点坐标.
解:(1)令y=0,可得:x﹣1=0,解得:x=1,
∴点A(1,0),
∵抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,
∴﹣1×2﹣1=﹣3,即点C(﹣3,0),
∴![]() ,解得:
,解得:![]()
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)∵点P在直线AB上方的抛物线上运动,
∴设点P(m,﹣m2﹣2m+3),
∵抛物线与直线y=x﹣1交于A、B两点,
∴![]() ,解得:
,解得:![]() ,
,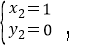
∴点B(﹣4,﹣5),
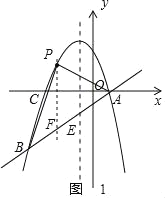
如图,过点P作PF∥y轴交直线AB于点F,
则点F(m,m﹣1),
∴PF=﹣m2﹣2m+3﹣m+1=﹣m2﹣3m+4,
∴S△ABP=S△PBF+S△PFA
=![]() (﹣m2﹣3m+4)(m+4)+
(﹣m2﹣3m+4)(m+4)+![]() (﹣m2﹣3m+4)(1﹣m)
(﹣m2﹣3m+4)(1﹣m)
=-![]() (m+
(m+![]() )2+
)2+ ![]() ,
,
∴当m=![]() 时,P最大,∴点P(
时,P最大,∴点P(![]() ,
,![]() ).
).
(3)当x=﹣1时,y=﹣1﹣1=﹣2,
∴点E(﹣1,﹣2),
如图,直线BC的解析式为y=5x+15,直线BE的解析式为y=x﹣1,直线CE的解析式为y=﹣x﹣3,
∵以点B、C、E、D为顶点的四边形是平行四边形,
∴直线D1D3的解析式为y=5x+3,直线D1D2的解析式为y=x+3,直线D2D3的解析式为y=﹣x﹣9,
联立![]() 得D1(0,3),
得D1(0,3),
同理可得D2(﹣6,﹣3),D3(﹣2,﹣7),
综上所述,符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案【题目】已知甲、乙两辆汽车分别从![]() 、
、![]() 两地同时匀速出发,甲车开往
两地同时匀速出发,甲车开往![]() 地,乙车开往
地,乙车开往![]() 地,设甲、乙两车距
地,设甲、乙两车距![]() 地的路程分别为
地的路程分别为![]() 、
、![]() (单位:
(单位:![]() ),甲车的行驶时间为
),甲车的行驶时间为![]() (单位:
(单位:![]() ).若甲车的速度为
).若甲车的速度为![]() ,
,![]() 与
与![]() 之间的对应关系如下表:
之间的对应关系如下表:
| 2 | 5 |
| 560 | 320 |
(1)分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;(不写
之间的函数关系式;(不写![]() 的取值范围)
的取值范围)
(2)当![]() 为何值时,甲、乙两辆汽车相遇?
为何值时,甲、乙两辆汽车相遇?
(3)当两车距离小于![]() 时,求
时,求![]() 的取值范围.
的取值范围.