题目内容
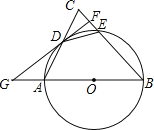
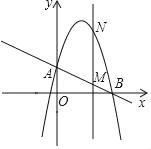
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )

A. ①②B. ①②③C. ①②③④D. ①③④
【答案】D
【解析】
①求出∠CAM=∠DEM=90°,根据相似三角形的判定推出即可;
②求出△BAE∽△CAD,得出比例式,把AC=![]() AB代入,即可求出答案;
AB代入,即可求出答案;
③通过等积式倒推可知,证明△PME∽△AMD即可;
④2CB2转化为AC2,证明△ACP∽△MCA,问题可证.
∵在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,
∴∠BAC=45°,∠EAD=45°,
∴∠CAE=180°-45°-45°=90°,
即∠CAM=∠DEM=90°,
∵∠CMA=∠DME,
∴△CAM∽△DEM,故①正确;
由已知:AC=![]() AB,AD=
AB,AD=![]() AE,
AE,
∴![]() ,
,
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD,
∴![]() ,即
,即![]() ,即CD=
,即CD=![]() BE,故②错误;
BE,故②错误;
∵△BAE∽△CAD
∴∠BEA=∠CDA
∵∠PME=∠AMD
∴△PME∽△AMD
∴![]() ,
,
∴MPMD=MAME,故③正确;
由②MPMD=MAME
∠PMA=∠DME
∴△PMA∽△EMD
∴∠APD=∠AED=90°
∵∠CAE=180°-∠BAC-∠EAD=90°
∴△CAP∽△CMA
∴AC2=CPCM
∵AC=![]() AB,
AB,
∴2CB2=CPCM,故④正确;
即正确的为:①③④,
故选D.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
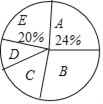
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?