Question

【题目】在一张矩形ABCD纸片中，AD=30,AB=25,先将这张纸片沿着过点A的直线折叠，使得点B落在矩形的对称轴上，折痕交矩形的边于点E，则折痕AE的长为_________.

Answer 1

【答案】或或

【解析】

点B是在以A点为圆心，AB为半径的圆上运动，圆与两条对称轴有3个交点，所以分3中情况进行讨论，由折叠的性质和勾股定理就能求得折痕AE的长．

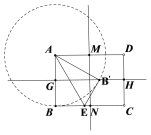
矩形的两条对称轴分解交矩形于点M，N，G，H，点B是在以A点为圆心，AB为半径的圆上运动，如图，

（1）当点B的对称点落在对称轴MN上时，

∵AD=30,AB=25，

∴AM=BN=15，

由折叠的性质可知，

，，

在中，由勾股定理得，

，

∴,

设，则EN=15-x，

在中，由勾股定理得

，解得：

，

由勾股定理得，

；

（2）当点在GH上时，如图，

∵点在矩形的对称轴上，

∴，

∴△是等边三角形，

∴∠BAE=30°，

∴；

（3）当点在NM的延长线上，如图，

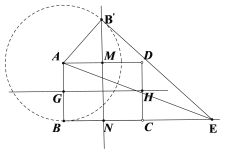
在中，由沟谷定理得，

，

∴，

设CE=x，则，

在中，由勾股定理得，

，解得，

，

∴，

故答案为：或或．