题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,过
上一点,过![]() 三点的
三点的![]() 交
交![]() 于
于![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(1)若![]() 是
是![]() 中点,连结
中点,连结![]() ,求证:四边形
,求证:四边形![]() 是平行四边形
是平行四边形
(2)连结![]() ,.当
,.当![]() ,且
,且![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
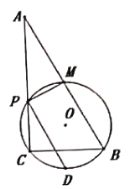
【答案】(1)证明见解析;(2)2.
【解析】
(1) 连结CM,PB,DM,根据圆内接四边形的性质得到∠BMP=90°,BP为⊙O的直径,再证明MD为⊙O的直径,最后证明PC∥MD,根据平行四边形的判定定理即可得到;
(2) 连结BD,先证四边形PDBM为矩形,再根据在Rt![]() 中,AC=4,tanA=
中,AC=4,tanA=![]() 即可求出答案;
即可求出答案;
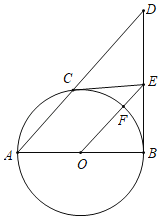
解(1)连结CM,PB,DM,

∵∠C=90°,四边形BCPM为圆内接四边形,
∴∠C+∠BMP=180°
∴∠BMP=90°,BP为⊙O的直径,
又PD∥AB,∴∠DPM=90°
∴MD为⊙O的直径
∵∠C=90°,M为AB的中点
∴CM=BM
∴弧CM=弧BM,又MD为⊙O的直径
∴DM垂直平分BC
∴PC∥MD,
∴四边形APDM为平行四边形(两组对边分别平行的四边形是平行四边形);
(2)如图,连结BD,CD

∵MD和BP均为⊙O的直径,
∴∠DPM=∠PMB=∠PDB=90°
∴四边形PDBM为矩形,
∴PM=BD
∵PM=PC
∴PC=BD,弧PC=弧BD
∴∠BPD=∠CDP(内错角相等,两直线平行),
∴BP∥CD
∴PD=BC
在Rt![]() 中,AC=4,tanA=
中,AC=4,tanA=![]() ,
,
∴BC=4tanA=2
∴PD=BC=2;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目