题目内容
【题目】菱形ABCD中，AB=8,∠B=120°，沿过菱形不同的顶点裁剪两次，再将所裁下的图形拼接，若恰好能无缝，无重叠的拼接成一个矩形，则所得矩形的对角线长为_____．
【答案】
或者
【解析】
按两种情况讨论，根据题意可知两种情况可拼出的新矩形一样，再根据菱形的性质以及矩形的性质，由勾股定理求解即可得到新矩形的对角线的长度；
解：分情况讨论，
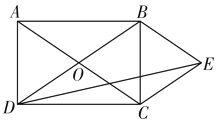
情况①，如图，分别沿菱形的对角线AC、BD裁剪，将剪下的四个三角形重新拼接得到矩形
或者矩形
，如图，
∵AB=8,∠B=120°，
∴
,
，
当拼成矩形时，有
,
,
∴矩形对角线长为：
，
当拼成矩形时，有
,
,
∴矩形对角线长为：
；
情况②，过B作BE⊥AD，过D作DF⊥BC，分别沿BE、DF裁剪，将剪下的三角形和剩余的矩形重新拼接得到和①一样的新矩形 或者矩形，如图，
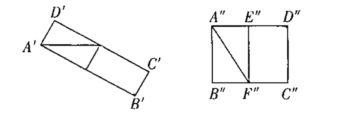
因此新矩形的对角线长为或者，
故答案为：或者；
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
