题目内容
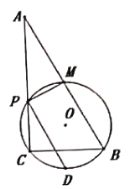
【题目】如图,AB为⊙O的直径,DB⊥AB于B,点C是弧AB上的任一点,过点C作⊙O的切线交BD于点E.连接OE交⊙O于F.
(1)求证:CE=ED;
(2)填空:
①当∠D= 时,四边形OCEB是正方形;
②当∠D= 时,四边形OACF是菱形.
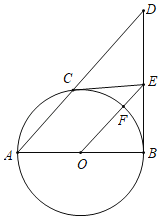
【答案】(1)见解析;(2)①45°;②30°
【解析】
(1)证明:连接OC,由CE为⊙O的切线,可得OC⊥CE,∠OCE=90°,所以∠ACO+∠DCE=90°,因为BD⊥AB,所以∠A+∠D=90°,又OA=OC,∠A=∠OCA,所以∠D=∠DCE,因此CE=ED;
(2)①若四边形OCEB是正方形,则∠CEB=90°,∠CED=90°,因为CE=ED,所以∠D=∠DCE=45°;
②若四边形OACF是菱形,则OA=AC,又OA=OC,于是△OAC为等边三角形,∠A=60°,因为DB⊥AB,所以∠A+∠D=90°,因此∠D=30°.
解:(1)证明:连接OC,
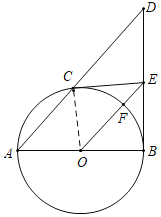
∵CE为⊙O的切线,
OC⊥CE,
∴∠OCE=90°,
∴∠ACO+∠DCE=90°,
∵BD⊥AB,
∴∠ABD=90°,
∴∠A+∠D=90°,
∵OA=OC,
∴∠A=∠OCA,
∴∠D=∠DCE,
∴CE=ED;
(2)若四边形OCEB是正方形,
则∠CEB=90°,
∴∠CED=90°,
∵CE=ED,
∴∠D=∠DCE=45°,
故答案为45°;
(3)若四边形OACF是菱形,
则OA=AC,
∵OA=OC,
∴△OAC为等边三角形,
∴∠A=60°,
∵DB⊥AB,
∴∠A+∠D=90°,
∴∠D=90°﹣60°=30°,
故答案为:30°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目