题目内容
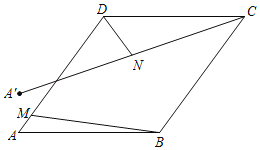
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 的各边作三个正方形,过点
的各边作三个正方形,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 中点,且
中点,且![]() ,则
,则![]() 的长为( )
的长为( )
A.8B.![]() C.
C.![]() D.12
D.12
【答案】D
【解析】
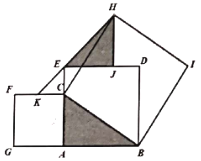
作HQ⊥AC,交AC的延长线于点Q,则四边形QEJH是矩形.设AB=a,AC=b,则CE=a-b.通过证明△QCH≌△ABC, 可证四边形QEJH是正方形,进而可证CE=CK,从而求出a和b的关系,然保护根据![]() 即可求出a的值.
即可求出a的值.
解:作HQ⊥AC,交AC的延长线于点Q,则四边形QEJH是矩形.设AB=a,AC=b,则CE=a-b.
∵∠QCH+∠ACB=90°,∠ABC+∠ACB=90°,
∴∠QCH=∠ABC,
∵∠Q=∠BAC=90°,CH=BC,
∴△QCH≌△ABC,
∴QH=AC=b,QC=AB=a,
∴QE=QC-CE=b,
∴QH=QE,
∴四边形QEJH是正方形,
∴∠CEK=∠QEH=45°,
∴△CKE是等腰直角三角形,
∴CE=CK.
∵![]() 为
为![]() 中点,
中点,
∴CE=CK=![]() ,
,
∴a-b=![]() ,
,
∴b=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴a=12,即AB的长是12.
故选D.


练习册系列答案
相关题目