题目内容
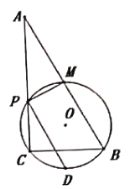
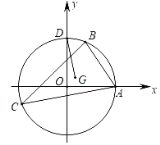
【题目】如图，半径为3的⊙O分别与x轴，y轴交于A，D两点，⊙O上两个动点B，C，使∠BAC＝45°恒成立，设△ABC的重心为G，则DG的最小值是_______．
【答案】
．
【解析】
连接AG并延长，交BC于点F，由三角形ABC的重心为G，可知F为BC的中点，再由垂径定理可知OF⊥BC，从而可求得OF的长；在AO上取点E，使AE=2EO，连接GE，可判定三角形AGE相似于三角形AFO，由相似三角形的性质列出比例式，求得GE的长，进而可得点E的坐标，利用勾股定理求出DE的长，根据G在以E为圆心，2为半径的圆上运动，可知DG的最小值为DE的长减去，计算即可.
解：连接AG并延长，交BC于点F.
∵△ABC的重心为G
∴F为BC的中点，
∴OF⊥BC，
∵∠BAC=45°
∴BOF=45°
∴OBF=45°
∴OF=BF=FC=
∵△ABC的重心为G，
∴AG=
AF.
在AO上取点E，使AE=AO，连接GE，
∴E（1，0）
∵.
∴△AGE∽△AFO，
∴
∴GE=
∴G在以E为圆心，为半径的圆上运动
∴DE=
∴DG的最小值为．
练习册系列答案
相关题目
