Question

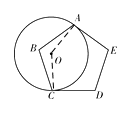
【题目】如图，半径为1的⊙O与正五边形ABCDE相切于点A、C ， 则弧AC的长为

A. π
B. π
C. π
D. π

Answer 1

【答案】C
【解析】解：连接OA，OC，
因为⊙O与正五边形ABCDE相切于点A、C ，
所以∠OAE=∠OCD=90°，
由多边形内角和公式可得正五边形的每个内角为（5-2）×180°÷5=108°，
所以∠AOC=540°-∠OAE-∠AED-∠EDC-∠DCO=144°，
则弧AC的长为.

故选C.
【考点精析】认真审题，首先需要了解正多边形的性质(正多边形都是轴对称图形．一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心;正多边形的中心边数为偶数的正多边形是中心对称图形，它的对称中心是正多边形的中心)，还要掌握多边形的对角线(设多边形的边数为n，则多边形的对角线条数为n(n-3)/2)的相关知识才是答题的关键．