题目内容
【题目】如图所示，某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°．若斜坡FA的坡比i=1： 
，求大树的高度．（结果保留一位小数）参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11， 取1.73．
【答案】解：过点D作DM⊥BC于点M，DN⊥AC于点N，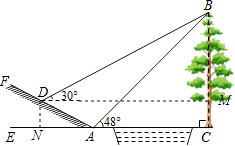
则四边形DMCN是矩形，
∵DA=6，斜坡FA的坡比i=1： 
，
∴DN= 
AD=3，AN=ADcos30°=6× 
=3 ，
设大树的高度为x，
∵在斜坡上A处测得大树顶端B的仰角是48°，
∴tan48°= 
≈1.11，
∴AC= 
，
∴DM=CN=AN+AC=3 + ，
∵在△ADM中， 
= 
，
∴x﹣3=（3 + ） ，
解得：x≈13．
答：树高BC约13米
【解析】首先过点D作DM⊥BC于点M，DN⊥AC于点N，由FA的坡比i=1： ，DA=6，可求得AN与DN的长，然后设大树的高度为x，又由在斜坡上A处测得大树顶端B的仰角是48°，可得AC= ，又由在△ADM中， = ，可得x﹣3=（3 + ） ，继而求得答案．
【考点精析】认真审题，首先需要了解关于仰角俯角问题(仰角：视线在水平线上方的角；俯角：视线在水平线下方的角)．
【题目】某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折．下表是购买量x（千克）、付款金额y（元）部分对应的值，请你结合表格：
购买量x（千克） | 1.5 | 2 | 2.5 | 3 |
付款金额y（元） | 7.5 | 10 | 12 | b |
（1）写出a、b的值，a= b= ；
（2）求出当x＞2时，y关于x的函数关系式；
（3）甲农户将18.8元钱全部用于购买该玉米种子，计算他的购买量．
