题目内容
【题目】解答题
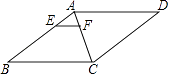
(1)如图1,在正方形ABCD中,点O是对角线AC的中点,点E是边BC上一点,连接OE,过点O作OE的垂线交AB于点F.求证:OE=OF. 
(2)若将(1)中,“正方形ABCD”改为“矩形ABCD”,其他条件不变,如图2,连接EF. ⅰ)求证:∠OEF=∠BAC.
ⅱ)试探究线段AF,EF,CE之间数量上满足的关系,并说明理由.
【答案】
(1)证明:(1)连接OB,
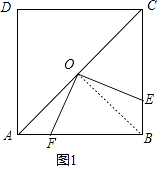
∵在正方形ABCD中,O是AC的中点,
∴OB=OA,∠OAB=∠OBA=∠OBC=45°,
∴∠AOB=90°,
又∵OE⊥OF,
∴∠AOF=∠BOE,
在△AOF和△BOE中, 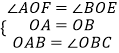 ,
,
∴△AOF≌△BOE,
∴OE=OF;
(2)①∵∠EOF=∠FBE=90°,
∴O,E,F,B四点共圆,
∴∠OBA=∠OEF,
∵在矩形ABCD中,O是AC的中点,
∴OA=OB,∠OAB=∠OBA,
∴∠OEF=∠BAC;
②如图,连接BD,延长EO交AD于G,

∵BD与AC交于O,
则△OGD≌△DEB,
∴OG=OE,
∴AG=CE,
∵OF⊥GE,
∴FG=EF,
在Rt△AGF中,GF2=AG2+AF2,即EF2=CE2+AF2.
【解析】(1)连接OB,更好正方形的性质得到OB=OA,∠OAB=∠OBA=∠OBC=45°,得到∠AOB=90°,根据全等三角形的判定和性质即可得到结论;(2)①根据已知条件得到O,E,F,B四点共圆,由圆周角定理得到∠OBA=∠OEF,根据矩形的性质即可得到结论;②如图,连接BD,延长EO交AD于G于是到OG=OE,根据线段的垂直平分线的性质得到FG=EF,根据勾股定理即可得到结论.
【考点精析】根据题目的已知条件,利用矩形的性质和正方形的性质的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案【题目】某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.下表是购买量x(千克)、付款金额y(元)部分对应的值,请你结合表格:
购买量x(千克) | 1.5 | 2 | 2.5 | 3 |
付款金额y(元) | 7.5 | 10 | 12 | b |
(1)写出a、b的值,a= b= ;
(2)求出当x>2时,y关于x的函数关系式;
(3)甲农户将18.8元钱全部用于购买该玉米种子,计算他的购买量.